Главная | Обратная связь

Статистическое определение вероятности.

Конспект лекций по

Теории вероятностей

 

Теория вероятностей.

Элементы комбинаторики

1. Принцип произведения.

Рассмотрим задачу: Сколькими способами можно доехать из пункта А в пункт В через пункт С, если из А в С ведут три дороги, а из С в В две дороги.

Введем обозначение: n – число способов. рис.

n= 2× 3 = 6 (вариантов).

Пример: В магазине 7 видов ручек и 5 видов блокнотов. Сколько различных подарков, состоящих из ручки и блокнота, можно составить?

n=7 × 5 =35

Принцип произведения: Если действие (испытание) можно разбить на отдельные этапы, причем число вариантов (исхода) на каждом отдельном этапе известно, то общее число вариантов равно произведению чисел вариантов на каждом этапе.

Если действие А можно осуществить n₁ способами, а действие В n₂ способами, то осуществить действия А и В можно n₁×n₂ способами. По решению задачи слову И соответствует знак умножения.

Пример: Сколько всего трехзначных чисел?

n=9×10×10=900 по принципу умножения комбинаторности.

Сколько пятизначных чисел делящихся на пять?

n=9×10×10×10×2=18000

Принцип сложения.

Если действие А можно осуществить n₁ способами, а действие В можно осуществить n₂ способами, то осуществить действия А или В можно n₁+n₂ способами.

По решению слову ИЛИ соответствует знак сложения.

Пример: В ящике 6 белых, 3 черных и 7 красных шаров. Сколькими способами можно вынуть один шар?

n=6+3+7=16 по принципу сложения комбинаторики.

Перестановки.

Пусть дано множество, состоящее из n-элементов. Множества, состоящие из этих же элементов, но отличающиеся порядком вхождения этих элементов, называется перестановками данного множества.

Рассмотрим множество из трех элементов {1;2;3}. Составим все перестановки данного множества: {1;3;2}{2;1;3}{2;3;1}{3;1;2}{3;2;1}, само множество тоже является перестановкой.

В общем случае число перестановок множества, состоящего из n-элементов, обозначается символом P_n . Число перестановок не зависит от характера элементов, а зависит от их количества.

Составить перестановки множества означает, что нужно произвести действие, состоящее из n-этапов, то есть один за другим в некотором порядке выписать все n-элементы множества.

По принципу произведения комбинаторики:
P_n =n×(n-1) × (n-2)…×1=n! ÞP_n=n!

Пример: Сколькими способами можно расставить 6 книг на книжной полке?

Пример: Сколькими способами можно рассадить четырех гостей за круглым столом?

4. Размещения.

Пусть дано множество, состоящее из n-элементов. Выберем из него упорядоченныеподмножества, состоящее из m элементов. Такие подмножества называются размещениями данного множества из n по m.

Пример: Возьмем множество, состоящее из 3^х элементов. Составим все размещения данного множества по два элемента в каждом.

{1,2,3}: {1;2}{1;3}{3;1}{2;3}{3;2}, получилось шесть размещений по два элемента в каждом.

Число размещений из n по m обозначается , где n – число элементов множества (объем совокупности), m - где n – число элементов подмножества (объем выборки).

Составить размещение из n-элементов по m, значит произвести действия, состоящие из m этапов.

=n(n-1)…(n–m+1)=

- число размещений из n по m.

Пример: Сколькими способами можно выбрать из 20 студентов 3^х дежурных так чтобы один из студентов был старшим?

Сочетания.

Пусть дано множество, состоящее из n элементов. Выберем из него неупорядоченные подмножества, состоящее из m элементов. Все такие подмножества называются сочетаниями данного множества из n по m.

Составим сочетания множества {1;2;3}, состоящие из двух элементов: {1;2}{1;3}{2;3}. В данном случае число сочетаний из трех элементов по два равно трем. Обозначается число сочетаний из n-элементов по m так: .

Для вычисления числа сочетаний проведем следующее размышление.

Размещения отличаются от сочетания наличием порядка в подмножестве.

Чтобы получить размещение с порядком надо взять сочетание без порядка и добавить порядок в подмножестве.

Из примера видно число сочетаний:

При решении задач часто используется следующие сочетания:
; ; ; ;

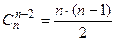
Вычислить сочетание, число сочетаний из 8 по 3.

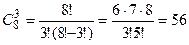
Случайное событие.

Наблюдение за многими процессами в технике, экономике и т.д. показывают, что некоторые параметры этих процессов не возможно выразить определенным числом. Например, число вызовов на АТС в течение часа не является строго определенной величиной, число деталей определенного размера среди серии изготовленных деталей не является строго определенной величиной. Все перечисленные величины являются случайными, то есть зависят от многих факторов.

Определение. Событие, которое в результате некоторых действий (испытаний) может произойти (наступить), а может не произойти, называется случайным событием.

Понятие случайного события является центральным в теории вероятности. Основная задача теории вероятности получить количественные оценки возможности появления следующего события.События обозначаются большими латинскими буквами A,B,C…

Статистическое определение вероятности.

Пусть в серии из n-одинаковых испытаний событие А наступило m раз. Относительной частотой появления события называется величина P*(A)=m*/n*(относительная частота).

Пример. Если при 7 подбрасываниях монеты орел выпадает 4 раза, то относительная частота появления орла при одном подбрасывании монеты P*(A)=4/7.

Если число испытаний невелико, то относительная частота появления события значительно отличается от других относительных частот при других испытаниях.

Если число испытаний очень велико, то относительные частоты появления одного и того же события мало отличаются друг от друга и их значения группируются возле некоторого числа. Другими словами, при n*®¥ относительная частота P*(A)®P – статистическое определение вероятности.

Пользоваться статистическим определением вероятности неудобно, так как при большом числе опытов не всегда можно точно провести подсчет.