 |
|
Случайные события, вероятность их наступления
Все наблюдаемые события можно разбить на три категории: достоверные, которые произойдут обязательно, невозможные, которые не могут произойти в данных условиях, и случайные, которые могут произойти, но могут и не произойти.
Достоверным событием является, например, следующее: при бросании игральной кости выпадет число от 1 до 6. Невозможным событием в тех же условиях является появление нуля очков. Случайным событием для этой игры является появление какого то числа от 1 до 6.
При рассмотрении случайных событий важнейшую роль играет понятие вероятности происхождения события. Если обозначит вероятность события A как P(A) и считать, что вероятность невозможного события равна нулю, а достоверного события - единице, то вероятность наступления случайного события 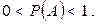
Случайные события бывают а) несовместные, б) единственно возможные, в) равновозможные.
Несовместными событиями называют такие события, когда появление одного исключает в одном испытании появление любого другого.
События называются единственно возможными, если достоверным событием является появление события только из этой группы.
События равновозможные, если ни одно из событий не является более вероятным по сравнению с любым другим.
Например, появление цифры и герба при одном подбрасывании рублевой монеты являются несовместным, ибо появление одного исключает появление другого. Эта пара событий является единственно возможной, так как одно из событий происходит обязательно, данные события равновозможны при качественно изготовленной монете.
Классическое определение вероятности.
Рассмотрим случайное событие A. Пусть из n единственно возможных, попарно несовместных, равновозможных исходов событие A происходит m раз (иногда говорят, что m - число благоприятствующих событию A исходов). Очевидно,
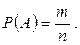
Итак, выпадение цифры 2 при одном бросании игральной кости имеет вероятность 1/6 , так как из возможных 6 событий благоприятствующим является только одно.
Задача. В ящике находится 10 шаров: 3 белых, 3 красных, 4 черных. Какова вероятность вынуть черный шар? Возможных исходов 10, благоприятствующих - 4. Вероятность 0,4.
Задача. В ящике 5 одинаковых кубиков. На всех гранях каждого кубика написана одна из букв О, П, Р, С, Т. Определить вероятность, что вынутые по одному и расположенные в процессе доставания в линию кубики образуют слово СПОРТ. Очевидно, число вариантов расположения кубиков в линию совпадает с числом перестановок пяти элементов, то есть равно 5! = 120. Благоприятствующее событие - появление слова СПОРТ - только одно, следовательно вероятность его появления - 1/120.
Задача. На стол брошены 2 игральные кости. Найти вероятность появления: а) шестерки хотя бы на одной из костей, б) суммы очков, равной 4, в) одинаковых цифр на обеих костях.
Всего событий 36, так как каждой цифре первой кости сопутствует шесть вариантов на второй.
а) благоприятствующие события: (1;6) , (2;6) , (3;6) , (4;6) , (5;6) , (6;6) , (6;1) , (6;2) , (6;3) , (6;4) , (6;5) . Вероятность события а) 11/36.
б) благоприятствующих исходов три: (1;3), (3;1), (2;2). Вероятность события б) 3/36.
в) благоприятствующих исходов шесть: (1;1), (2;2), (3;3), (4;4), (5;5), (6;6). Вероятность события в) 6/36.
Задачи для домашней работы
1. Брошена игральная кость. Найти вероятность, что выпадет четное число.
2. Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 100. Какова вероятность, что первый вынутый жетон не содержит цифры 5?
3. Из полного набора костей домино (28 косточек) вынимается одна. Какова вероятность того, что на вынутой кости шесть очков?
4. На столе экзаменатора 20 билетов. Какова вероятность того, что первый экзаменующийся вынет билет с двузначным номером?
Статистическое определение вероятности.
Классическое определение вероятности события очень удобно в применении, но только в тех случаях, когда число событий конечно и сравнительно невелико и когда происходящие события равновозможны. На практике, однако, часто встречаются случаи, когда число возможных исходов в испытаниях бесконечно. Не всегда удается оценить равновозможность событий. Обычно, она вытекает из соображений симметрии и равномерности. Так, возможность использования классического определения вероятности при игре в кости реализуется только, если кость представляет собой правильный шестигранник, изготовленный из однородного материала. Конечно, при игре в кости эти требования обязательны, и подсчитывать вероятность по классической формуле можно. Но уже при стрельбе из какого то оружия вышеупомянутые требования выполняются не всегда. Это зависит от качества, скажем, патронов, от погодных условий и т.д. При невозможности использования классического определения вероятности вводят понятие статистической вероятности, или относительной частоты появления события. Если классическое определение может использоваться до проведения испытаний, то статистическое связано с самими испытаниями, а статистическая вероятность события устанавливается по результатам проведенных испытаний. Например, статистическая вероятность помогает определить процент бракованных деталей, изготовляемых на некотором производстве. Определив отношение бракованных деталей к числу всех изготовленных деталей за какой то день недели, можно спрогнозировать качество произведенной работы за неделю, месяц и т.д. Совершенно очевидно, что определить достаточно точно статистическую вероятность можно только при достаточно большом количестве испытаний, чем их больше, тем точнее результат. Немаловажна и устойчивость появления события в различных сериях испытаний.
Если в конкретных испытаниях реализуются условия, в которых возможно использование классической вероятности, то с ростом числа испытаний статистическая вероятность события стремится к классической.
Геометрическое определение вероятности.
Наряду с классическим определением вероятности, кроме статистической, используется еще и геометрическая вероятность. Она применима к бесконечному числу случайных событий.
Рассмотрим следующую ситуацию. Пусть имеется отрезок длины L, отрезок длины l расположен внутри отрезка L, неважно, в какой его части. Поставленная точка может оказаться с равной вероятностью в любом месте отрезка L. Как вычислить вероятность того, что точка окажется на отрезке дины l? При указанных условиях вероятность будет совпадать с отношением длин этих отрезков, то есть l/L. Если задача двумерная, то вероятность - есть отношение площадей фигур.
Задача. Имеется отрезок OA длины L. На отрезок случайным образом попадает точка B. Какова вероятность того, что длина наименьшего из отрезков OB и AB будет: а) больше L/3, б) меньше L/3?
Решение. Разделим отрезок OA на три равные части OC, CD, DA. Благоприятствующим исходом события а) является расположение точки B на отрезке CD. Но длина отрезка CD равна L/3. Следовательно, вероятность события а) равна L/3/L= 1/3. Выполнение условия б) реализуется, если точка попадает либо на OC, либо на DA. Суммарная длина этих отрезков равна 2L/3 и представляет собой благоприятствующий событию исход. Следовательно, вероятность события б) равна 2/3.