 |
|
Интеграл с бесконечным промежутком интегрирования (несобственный интеграл 1 рода)
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
Определенный интеграл
,
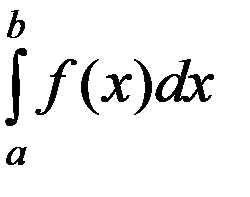где [a;b]–ограниченный промежуток, f(x) 
С[a;b], называется собственным интегралом.
Интеграл с бесконечным промежутком интегрирования (несобственный интеграл 1 рода)
Пусть f(x) 
С[a; +∞). Предел
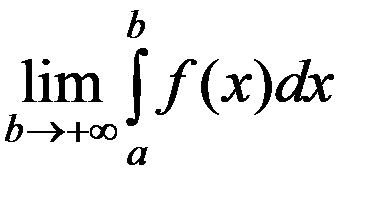(1)
называется несобственным интегралом 1 рода:
.
Если предел (1) конечный, то несобственный интеграл
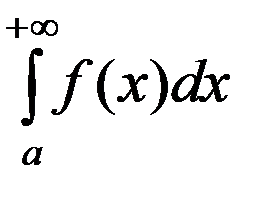(2)
сходится. Если предел (1) бесконечен или не существует, то интеграл (2) расходится.
Аналогично определяется несобственный интеграл на [–∞; b):
.
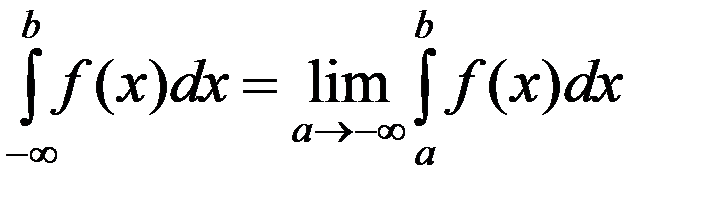Несобственный интеграл на R:
,
где с – произвольное число.
Интеграл слева сходится тогда, когда сходятся оба интеграла справа.
Если f(x) ≥0 на [a; +∞) и интеграл
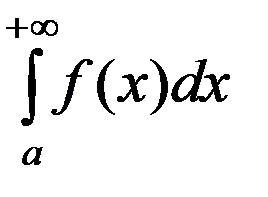
сходится, то он представляет площадь бесконечно длинной криволинейной трапеции.
Пример 1. Вычислить или установить расходимость
▼
1) 
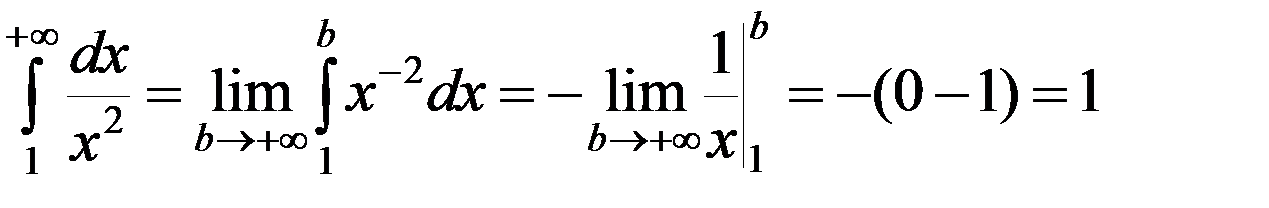– интеграл сходится;
2) 
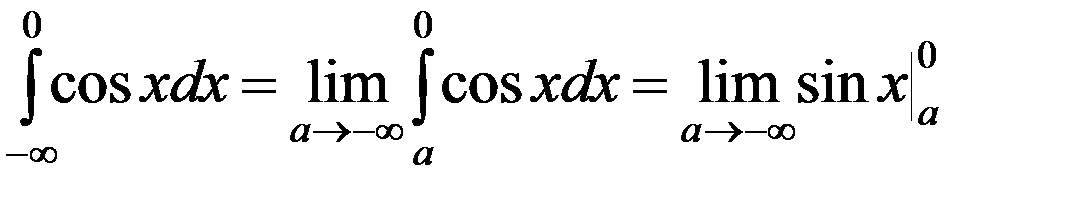– интеграл расходится, так как 
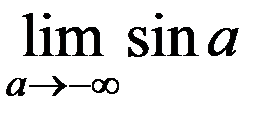– не существует;
3) 
– интеграл расходится.
▲
В некоторых задачах нет необходимости вычислять интеграл: достаточно знать его сходимость или расходимость.
Теорема 1.(Признак сравнения).Пусть f(x), φ(x)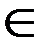 
С[a; ∞), 0 ≤f(x) ≤ φ(x) 
[a; ∞).
Тогда 1) из сходимости интеграла 
следует сходимость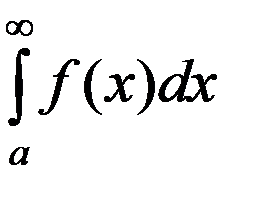 
;
2) из расходимости интеграла 
следует расходимость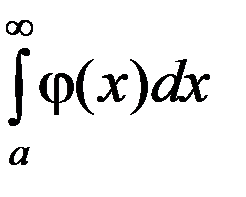 
.
Док. ▼ Пусть 
сходится и равен М; тогда 
b 
R+.
В соответствии со свойством 7 об интегрировании неравенств
.
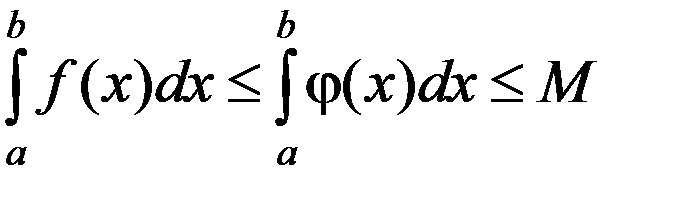Следовательно
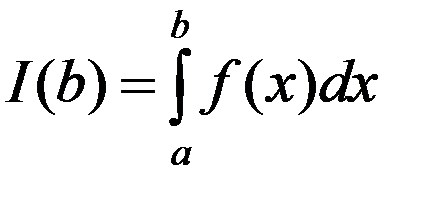– ограниченная функция и интеграл 
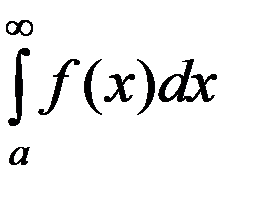сходится.
Если дано, что 
расходится, то
.
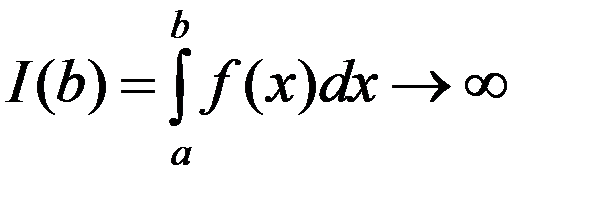Так как
,
то и
.
Следовательно,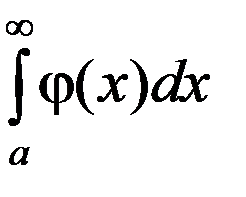 
– расходится.
▲
Пример 2. Исследовать сходимость интеграла
.
Решение ▼
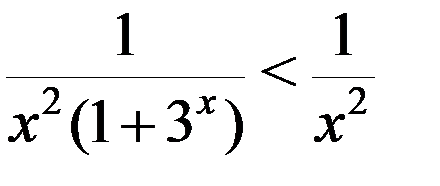
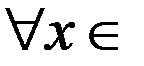[1; +∞).
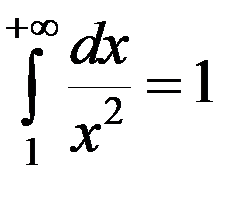
- сходится (причем, его значение <1).
▲
Признак сравнения относится только к функциям, сохраняющим знак на бесконечном промежутке интегрирования.
Более сложным является исследование интегралов от функций, несохраняющих знак, например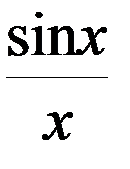 
.
Признак сходимости, позволяющий сводить исследование к случаю положительных функций.
Если сходится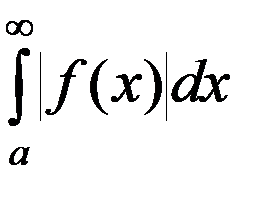 
, то сходится и 
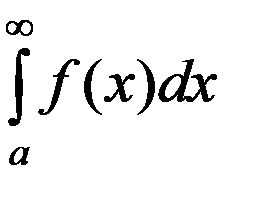. При этом интеграл 
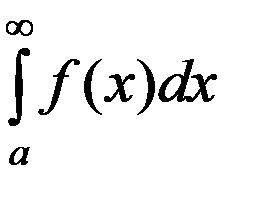называется абсолютно сходящимся.
_______________________________
Теорема 2.Если существует предел
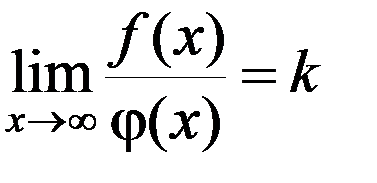, k R+, f(x) >0, φ(x) >0,
то интегралы 
и 
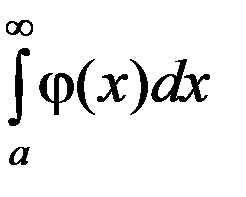одновременно сходятся или одновременно расходятся (т.е. ведут себя одинаково в смысле сходимости).
_______________________________
Пример 3. Исследовать сходимость интеграла
.
Решение ▼
.
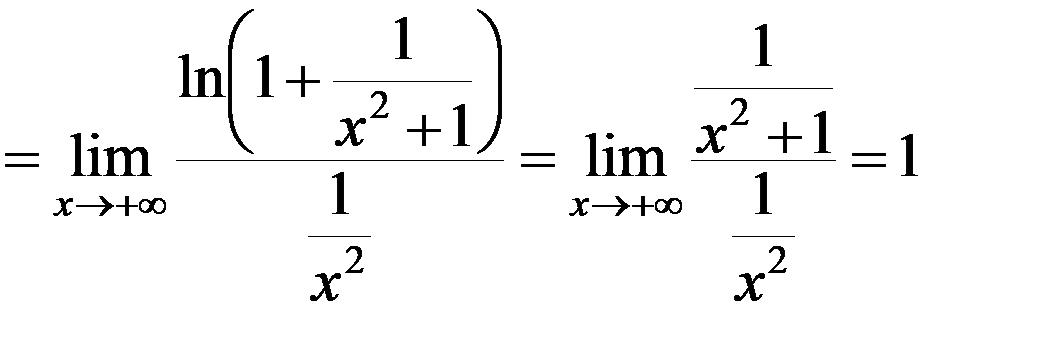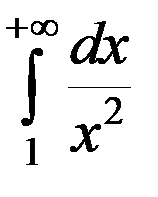- сходится 
- сходится.
▲