 |
|
Определение усилий в стержнях, вызванных действием внешней нагрузки
РАСЧЕТЫ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СТЕРЖНЕВЫХ СИСТЕМ НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ ПРИ РАСТЯЖЕНИИ И СЖАТИИ
Отчет по расчетно-проектировочной работе №2
по дисциплине сопротивление материалов
Выполнил студент группы СМ-14-2 П.А.Чернышев
Принял В.П.Ященко
Иркутск 2015
Цель работы:
1) Определить усилия в стержнях, вызванные действием внешней нагрузки;
2) Из расчета на прочность по допустимым напряжениям определить безопасные размеры круглого поперечного сечения стержней (d1 и d2);
3) Произвести деформационную проверку результатов;
4) Определить усилия в стержнях, вызванные неточностью изготовления второго стержня (стержень короче расчетной длины);
5) Определить усилия в стержнях, вызванные нагревом первого стержня.
Дано: Абсолютно жесткая балка закреплена с помощью неподвижного цилиндрического шарнира и двух стержней. Длина 1-го стержня l1 = 2 м, длина 2-го стержня l2 = 1.8 м. Угол между 1-м стержнем и балкой равен β = 30о, между 2-м стержнем и балкой равен α = 45о. Расстояния a, b и c равны соответственно 0.9 м, 0.7 м и 1.2 м. Площади стержней А1/ А2 = n = 2. Сила F равна 35 кН. Также действует распределенная нагрузка интенсивностью q = 40 кН/м. (см. рисунок 1 в приложении А).
Данные по материалу:
1 стержень – латунь, модуль Юнга E1 = 105 МПа, так как материал – пластичный, то σu – не определен, следовательно, необходимо знать предел текучести, а он равен σy1 = 150 МПа, нормативный коэффициент запаса прочности [n] = 1.5, коэффициент линейного расширения α1 = 165*10-7 1/град;
2 стержень – сталь, модуль Юнга E2 = 2*105 МПа, так, как и этот материал – пластичный, то σu – также не определен, следовательно, также необходимо знать предел текучести, а для данной марки стали он равен σy2 = 240 МПа, нормативный коэффициент запаса прочности [n] = 1.5, коэффициент линейного расширения α2 = 125*10-7 1/град;
Неточность изготовления 2-го стержня δ2 = 0.5 мм (стержень короче расчетной длины);
Изменение температуры 1-го стержня Δt1 = 30 K (нагрев).
Определение усилий в стержнях, вызванных действием внешней нагрузки
Для начала сделаем следующее: отметим на рисунке 1 (приложение А) точки B, C и D так, что BC = a и CD = b + c. Следовательно, длина всей балки будет равна BD. Это понадобится для удобства дальнейшего решения задачи (особенно для составления плана перемещений).
Итак, сперва определим, что происходит с каждым из стержней. Для этого посчитаем моменты сил относительно неподвижной опоры B для силы F и для силы интенсивности Q (Q = q*a):
ΣMBF = - F*(a + b) = - 35*1.6 = - 56 кН*м (балка стремится повернуться по часовой стрелке)
ΣMBQ = + Q*  = q*a*a/2 = 40*0.9*0.9/2 = + 16.2 кН*м (балка стремится повернуться против часовой стрелки)
= q*a*a/2 = 40*0.9*0.9/2 = + 16.2 кН*м (балка стремится повернуться против часовой стрелки)
Так как |MBF| > |MBQ|, то в итоге балка будет стремиться повернуться по часовой стрелке, следовательно, стержень 1 будет испытывать растяжение, и стержень 2 – сжатие.
Далее необходимо составить план сил(см. рисунок 2 в приложении А).
И уже после этого, составим, соответственно, уравнения статики для данной системы:

ΣXi = 0: HB – N1*cosβ + N2*cosα = 0 (1)
ΣYi = 0: - F + RB – Q + N1*sinβ + N2*sinα = 0 (2)
ΣMB = 0: - F*(a + b) + N1*(a + b + c)*sinβ – Q*a/2 + N2*a*sinα = 0
Выразим из уравнения моментов N1. Для этого подставим уже известные значения сил F и Q:
-35*(0.9 + 0.7) + N1*(0.9 + 0.7 + 1.2)*sin30o – 36*0.9/2 + N2*0.9*sin45o = 0
N1*(0.9 + 0.7 + 1.2)*sin30o = 35*1.6 + 36*0.9/2 - N2*0.9*sin45o
N1 = (35*1.6 + 36*0.9/2 - N2*0.9*sin45o)/ (2.8*sin30o)
N1 = (72.2 - N2*0.636)/1.4
Отсюда N1 = 51.57 – 0.45* N2(3)
Таким образом, мы имеем дело со статически неопределимой системой уравнений, где количество неизвестных усилий m = 4 (HB, RB, N1 и N2) и количество уравнений равновесия n = 3. Следовательно, степень статической неопределимости данной системы равна S = m – n = 4 – 3 = 1. Это означает, что такая система уравнений один раз статически неопределима.
Чтобы решить эту систему нужно для начала составить план перемещений (см. рисунок 3 в приложении А).
1 стержень: деформация Δl1 = DD2 – удлинение стержня
2 стержень: деформация Δl2 = CC2 – укорочение стержня
Геометрическая часть задачи:
Рассмотрим треугольники BCC1 и BDD1: так как CC1 || DD1 и угол DBD1 – общий, то в треугольнике BDD1 углы BCC1 и BC1C будут равны соответственно углам BDD1 и BD1D в треугольнике BDD1. Следовательно, треугольники BCC1 и BDD1– подобны(по II признаку подобия).
Следовательно,  =
= 
Теперь рассмотрим прямоугольные треугольники CC2C1 и DD2D1 (см. также рисунок 3 в приложении А):
CC1 = CC2/sinα = Δl2/sinα и DD1 = DD2/sinβ = Δl1/sinβ
Отсюда следует, что:
 =
=  – уравнение совместности деформаций (4)
– уравнение совместности деформаций (4)
Физическая часть задачи:
 |
Δl1 = N1*l1/E1*A1 (5)

Δl2 = N2*l2/E2*A2 (6)
Синтез уравнений:
Подставляем уравнения (5), (6) в уравнение (4):
N1*l1/(E1*A1*sinβ*BD) = N2*l2/(E2*A2*sinα*BC)
Отсюда
N2 = (N1*l1* E2*A2*sinα*BC)/(l2*E1*A1*sinβ*BD)
Так как A1 = 2*A2 и E2 = 2*E1, заменим эти величины:
N2 = (N1*l1*2*E1*A2*sinα*BC)/(l2*E1*2*A2*sinβ*BD)
Сократив величины A и E, получаем, что:
N2 = (N1*l1*2*sinα*BC)/(l2*2*sinβ*BD) = N1*(l1*2*sinα*BC)/(l2*2*sinβ*BD) = N1*(2*2*sin45о*0.9)/(1.8*2*sin45о*2.8)
Отсюда N2 = 0.505*N1(7)
Теперь имеем систему уравнений (3) и (7) – с двумя неизвестными
 |
N2 = 0.505*N1
N1 = 51.57 – 0.45*N2
Подставляя уравнение (7) в уравнение (3), находим усилие N1:
N1 = 51.57 – 0.45*0.505* N1
1.227*N1 = 51.57
Отсюда N1 = 51.57/1.227 = 42029 Н = 42.029 кН
Следовательно, N2 = 0.505*N1 = 0.505*42.029 = 21.225 кН
2 Из расчета на прочность по допустимым напряжениям определить безопасные размеры круглого поперечного сечения стержней (d1 и d2)
Производим расчет на прочность:
Условие прочности: σmax = Nmax/A ≤ [σ], отсюда A ≥ Nmax/[σ]
Рассчитаем допустимые напряжения для стержней:
1 стержень: [σ1] = σ0/[n] = σy1/[n] = 150/1.5 = 100 МПа (латунь)
2 стержень: [σ2] = σ0/[n] = σy2/[n] = 240/1.5 = 160 МПа (сталь)
Из условия прочности:
A1 ≥ N1/ [σ1]
Следовательно, A1 ≥ 42.029*103/(100*106) = 0.42*10-3 м2
Из соотношения площадей n = A1/A2 = 2 следует, что
A2 = A1/2= 0.42*10-3/2 = 0.21*10-3 м2
Теперь необходимо проверить, обеспечена ли прочность для 2-го стержня (для 1-го она, очевидно, обеспечена):
σ2 = N2/A2 = 21.225*103/0.21*10-3 = 101.07 МПа < [σ2]
Следовательно, прочность обеспечена для обоих стержней.
Теперь можно определить диаметры d1 и d2 для этих стержней:
d1=  =
= 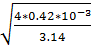 ≈ 0.023 м ≈ 23 мм
≈ 0.023 м ≈ 23 мм
d2 =  =
=  ≈ 0.016 м ≈ 16 мм
≈ 0.016 м ≈ 16 мм