 |
|
Преобразования Фурье.
Имени академика М.Ф. Решетнева»
(СибГАУ)
УТВЕРЖДАЮ
Заведующий кафедрой
Ф.И.О. (подпись)
«» 2011г.
Кафедра ЭТТ
Реферат
Преобразование Фурье
Проверил:
Филимонов
Выполнил:
ст.группы БТК-92
Батаркин А.А.
Красноярск, 2011г.
Преобразования Фурье.
Преобразование Фурье — операция, сопоставляющая функции вещественной переменной другую функцию вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие — гармонические колебания с разными частотами.
Преобразование Фурье общего вида функции f вещественной переменной можно представить интегральным преобразованием:
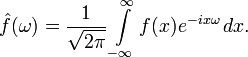
Преобразование Фурье используется во многих областях науки — в физике, теории чисел, комбинаторике, обработке сигналов, теории вероятностей, статистике, криптографии, акустике, океанологии, оптике, геометрии, и многих других. В обработке сигналов и связанных областях преобразование Фурье обычно рассматривается как декомпозиция сигнала на частоты и амплитуды, то есть, обратимый переход от временного пространства в частотное пространство. Богатые возможности применения основываются на нескольких полезных свойствах преобразования:
Преобразования являются линейными операторами и, с соответствующей нормализацией, также являются унитарными (свойство, известное как теорема Парсеваля или, в более общем случае как теорема Планшереля, или в наиболее общем как дуализм Понтрягина).
Преобразования обратимы, причём обратное преобразование имеет практически такую же форму, как и прямое преобразование.
Синусоидальные базисные функции являются собственными функциями дифференцирования, что означает, что данное представление превращает линейные дифференциальные уравнения с постоянными коэффициентами в обычные алгебраические. (Например, в линейной стационарной системе частота — консервативная величина, поэтому поведение на каждой частоте может решаться независимо.)
По теореме о свёртке, преобразование Фурье превращает сложную операцию свёртки в простое умножение, что означает, что они обеспечивают эффективный способ вычисления основанных на свёртке операций, таких как умножение многочленов и умножение больших чисел.