 |
|
Преобразование Фурье над конечным полем
Дискретное преобразование Фурье над конечным полем — это один из видов дискретного преобразования Фурье для вектора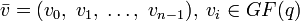 
над конечным полем GF(q), определяемое как вектор 
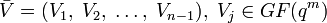, где n делит qm − 1 при некотором целом положительном m, с компонентами, вычисляемыми как 
где α — элемент порядка n в поле GF(qm) (то есть такой, что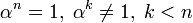 
).
Индекс i можно назвать временем, а 
— временной функцией или сигналом. Аналогично индекс j — частотой, а — 
частотной функцией или спектром.
Обратное преобразование в данном случае определяется таким образом 
где n интерпретируется как элемент (число) по модулю характеристики p поля GF(q), то есть 
.
Другие варианты
Дискретное преобразование Фурье является частным случаем (и иногда применяется для аппроксимации) дискретного во времени преобразования Фурье (DTFT), в котором xk определены на дискретных, но бесконечных областях, и таким образом спектр является непрерывным и периодическим. Дискретное во времени преобразование Фурье является по существу обратным для рядов Фурье.
Эти разновидности преобразования Фурье могут быть обобщены на преобразования Фурье произвольных локально компактных абелевых топологических групп, которые изучаются в гармоническом анализе; они преобразуют группу в её дуальную группу. Эта трактовка также позволяет сформулировать теорему свёртки, которая устанавливает связь между преобразованиями Фурье и свёртками. См. также дуализм Понтрягина.
Интерпретация в терминах времени и частоты
В терминах обработки сигналов, преобразование берёт представление функции сигнала в виде временны́х рядов и отображает его в частотный спектр, где ω — угловая частота. То есть оно превращает функцию времени в функцию частоты; это разложение функции на гармонические составляющие на различных частотах.
Когда функция f является функцией времени и представляет физический сигнал, преобразование имеет стандартную интерпретацию как спектр сигнала. Абсолютная величина получающейся в результате комплексной функции F представляет амплитуды соответствующих частот (ω), в то время как фазовые сдвиги получаются как аргумент этой комплексной функции.
Однако важно осознавать, что преобразования Фурье не ограничиваются функциями времени и временными частотами. Они могут в равной степени применяться для анализа пространственных частот, также как для практически любых других функций.
Вывод:
Преобразование Фурье, первоначально возникшее в теории теплопроводности, имеет многочисленные применения как в самой математике (например, при решении дифференциальных, разностных и интегральных уравнений, в теории специальных функций и т.д.), так и в различных разделах теоретической физики. Например, преобразование Фурье стало стандартным аппаратом квантовой теории поля, широко используется в методе функций Грина для неравновесных задач квантовой механики и термодинамики, в теории рассеяния и т.д.
Подводя итог можно сказать, что преобразование Фурье очень полезно для большого числа современных наук, тем самым Фурье внес немалый вклад в развитие научной деятельности всего человечества.