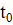|
|
Источники с нормальным законом распределения плотности мощности
Электрическая дуга, излучение лазера, плазма, пучок электронов имеют распределенную плотность мощности в пятне нагрева близко к закону распределения
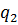 (r)=
(r)=  гаусовское распределение
гаусовское распределение

По закону нормального распределения плотность мощности максимальна в точек О и равна  ,которая с увеличением r уменьшаеться и стремиться к нулю на бесконечности.Для сварочных источников принимают эффективное пятно нагрева радиусом
,которая с увеличением r уменьшаеться и стремиться к нулю на бесконечности.Для сварочных источников принимают эффективное пятно нагрева радиусом  .При
.При 
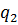 (
(  )=
)= 
Вычисляеться  при нормальном распределении
при нормальном распределении
q=  ·2Пrdr=
·2Пrdr=  =
=  ·2
·2  =
=  ·
· 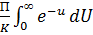 =
=
 ·
·  (
(  +
+  )=
)=  ·
·  (0+1)=
(0+1)=  ·
· 
Источники с нормальным распределением можно заменить эквивалентными по мощности источником с равномерным распределением плотности мощности  и
и 

q=  ·
·  ·
· 
 =
=  ·
·  ·
·  =
=  ·
· 
 =
=  ,где k – коэффициент сосредоточенности источника с нормальным распределением .k [
,где k – коэффициент сосредоточенности источника с нормальным распределением .k [  ]
]
В ТСП при расчете температурных полей используют точеченые источники,то есть источники с выделением энергии на бесконечно малой площади или в бесконечно малом объеме.
Линейный источник – равномерно распределенный по длине отрезка.
Расчеты температурных полей при различных схемах воздействующих сварочных источников
Классическую теорию тепловых процессов сварки разработал Рыкалин Н.Н.
1. Мгновенные точечные источники .
Мгновенные точечные источники воздействуют во время t=0 и в бесконечно малом объеме dxdydz.
-полубесконечное тело.
Мгновенный источник Q действует на поверхность полубесконечного тела в точке о(начало системы координат x,y,z)
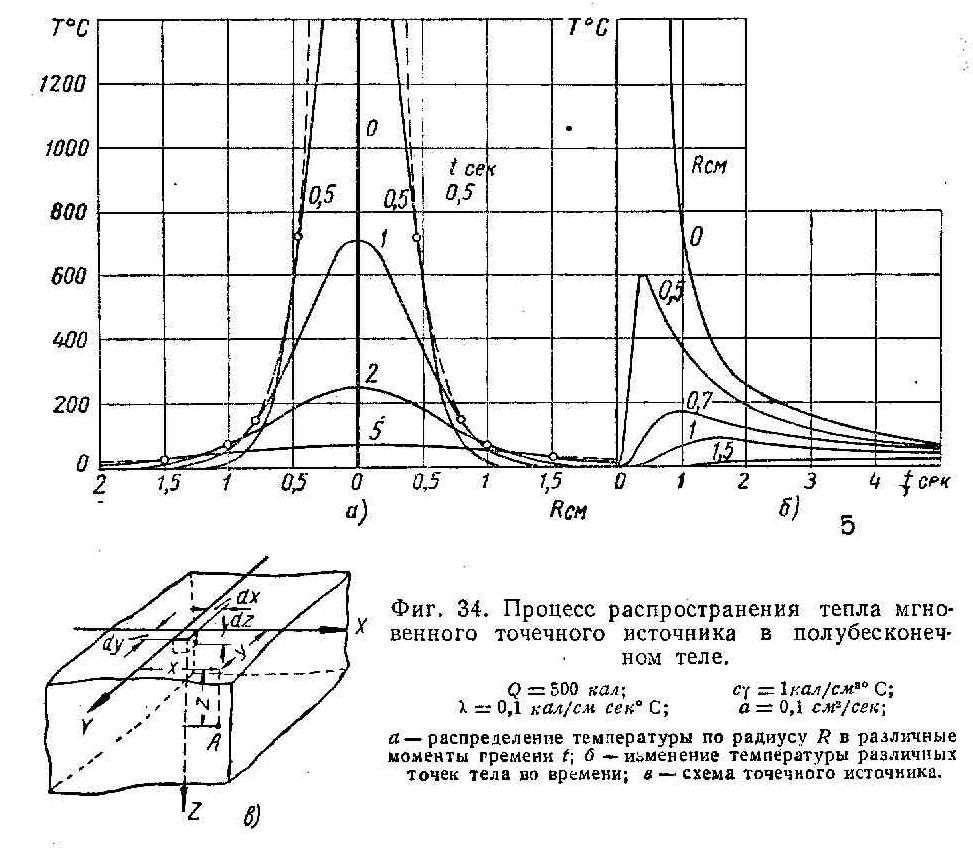
R= 
Расперделение температуры в полубесконечном теле от мгновенного точечного источника выражаеться как
T(R,t)= 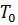 +
+ 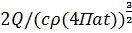 - температура остывания для мгновенного линейного источника в бесконечной пластине.
- температура остывания для мгновенного линейного источника в бесконечной пластине.
Мгновенные истчники в массивном теле,пластине.
r= 
T(r,t)= 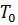 +
+  e(-
e(-  - bt),
- bt),
b – коэффициент поверхностной теплоотдачи пластины (температуроотдачи)
b= 
α – коэффициент поверхностной теплоотдачт
Для плоского мгновенного источника действующего в стержне посомтреть самостоятельно.
2. Неподвижные непрерывнодействующие источники.
Уравнения получают используя принцип наложения ,то есть непрерывнодействующий источник можно рассматривать как совокупность мгновенных ,выражение температуры получаем интегрированием элементарных приращений температур от мгновенных источников .Температура в полубесконечном теле от непрерывного источника ;
T(R,t)= 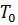 +
+  e(-
e(-  )d
)d 
t-время действия источника
 -момент действия мгновенного источника
-момент действия мгновенного источника
Все формулы работают при t>0
-для пластины получаем
T(r,t)=  +
+  e(-
e(-  d
d 
3.Непрерывнодействующие подвижные источникик.
Подвижные источники можно также рассматривать как совокупность мгновенных источников постепенно изменяющих свое положение ,например вдоль оси x

Источник движеться из точки 
 – неподвижная система ,связанная с полубезконечным телом,источник начал действовать при t=0, в точке
– неподвижная система ,связанная с полубезконечным телом,источник начал действовать при t=0, в точке  , подвижная система Oxyz связана с точечным источником ,точечный источник в точке О ,температура от непрерывнодвигающего с постоянной скоростью источника определяеться так же с использованием многодействующего точечного источника в момент времени
, подвижная система Oxyz связана с точечным источником ,точечный источник в точке О ,температура от непрерывнодвигающего с постоянной скоростью источника определяеться так же с использованием многодействующего точечного источника в момент времени  выделяеться количество теплоты dq
выделяеться количество теплоты dq
dq=dq 
эта энергия подставляеться в выражение t от мгновенного источника и беретсяинтеграл.В результате ,согласно принципу наложения получаем температурное поле неподвижной системе координат
T( 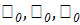 ,t)=
,t)=  +
+  e(
e( 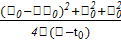 )d
)d 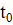
Соответственно получают уравнение температуры в подвижной системе координат,учитывая что
x=  -vt : y=
-vt : y=  :z=
:z= 
T(x,y,z,t)=  +
+  e
e  )
) 
Для пластины толщиной  в неподвижной системе координат:
в неподвижной системе координат:
T( 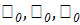 ,t)=
,t)=  +
+  e(
e( 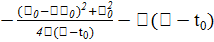 )d
)d 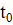
T(x,y,t)=  +
+ 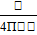 e
e  )
)  ) d
) d