 |
|
Экономический смысл двойственной модели.
Двойственная ЗЛП
Рассмотрим ЗЛП:
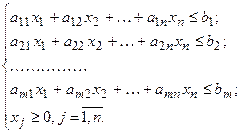
Двойственная ЗЛП имеет вид:
В двойственной задаче требуется найти минимум целевой функции, ограничения – неравенства со знаком 
, управляющие переменные 
неотрицательны. Задача содержит 
управляющих переменных и 
ограничений. Коэффициенты целевой функции задачи 
являются свободными членами исходной задачи, а свободные члены двойственной задачи 
- коэффициентами целевой функции исходной ЗЛП. Матрица коэффициентов двойственной задачи транспонирована.
ЗЛП и ДЗЛП называются парой взаимно двойственных задач линейного программирования.
Теорема двойственности
Если одна из взаимно двойственных задач имеет оптимальное решение 
, то другая также имеет оптимальное решение 
. При этом соответствующие им оптимальные значения функций 
и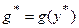 
равны.
Экономический смысл двойственной модели.
Пусть в качестве управляющих переменных 
исходной модели рассматривается число изделий, производимых некоторым предприятием, а в качестве параметров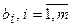 
- количество ресурсов 
-го типа, используемых для изготовления изделий. Через 
обозначено количество ресурсов -го типа, идущее на изготовление одного изделия 
-го вида ( 
- прибыль от реализации одного изделия -го вида). Тогда исходная модель соответствует задаче определения оптимального плана производства продукции, обеспечивающего максимальную прибыль.
Пусть предприятие решило прекратить производство изделий и продать ресурсы, идущие на их изготовление. Обозначим через 
цены на единицу ресурсов -го вида, 
. Цены на ресурсы должны удовлетворять следующим двум условиям: во-первых, они не должны быть слишком высокими, иначе ресурсы невозможно будет продать; во-вторых, цены на ресурсы должны быть такими, чтобы прибыль от их реализации была больше прибыли от реализации готовой продукции. Первое условие выражается формулой
.
Второе условие - ограничениями
В левой части каждого из неравенств стоит прибыль от продажи ресурсов всех типов, идущих на изготовление -го изделия, в правой части – прибыль от продажи -го изделия, 
. Таким образом, двойственная задача соответствует следующей экономической проблеме: по каким минимальным ценам следует продавать ресурсы, чтобы прибыль от их реализации была больше прибыли, полученной от реализации продукции, изготавливаемой с использованием этих ресурсов.
Значение переменных , , часто называют теневыми ценами.
Построение двойственной задачи позволяет глубже разобраться в поставленной экономической проблеме.
Между прямой и двойственной задачами можно установить следующую взаимосвязь:
1. Если прямая задача на максимум, то двойственная к ней — на минимум, и наоборот.
2. Коэффициенты 
целевой функции прямой задачи являются свободными членами ограничений двойственной задачи.
3. Свободные члены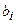 
ограничений прямой задачи являются коэффициентами целевой функции двойственной.
4. Матрицы ограничений прямой и двойственной задач являются транспонированными друг к другу.
5. Если прямая задача на максимум, то ее система ограничений представляется в виде неравенств типа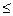 
. Двойственная задача решается на минимум, и ее система ограничений имеет вид неравенств типа .
6. Число ограничений прямой задачи равно числу переменных двойственной, а число ограничений двойственной — числу переменных прямой.
7. Все переменные в обеих задачах неотрицательны.
Основные теоремы двойственности и их экономическое содержание
Теорема. Для любых допустимых планов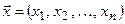 
и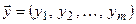 
прямой и двойственной ЗЛП справедливо неравенство 
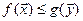, т.е.
– основное неравенство теории двойственности.
Теорема (критерий оптимальности Канторовича). Если для некоторых допустимых планов 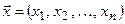и 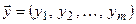пары двойственных задач выполняется равенство 
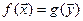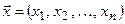, то и 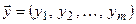являются оптимальными планами соответствующих задач.
Теорема (малая теорема двойственности).Для существования оптимального плана любой из пары двойственных задач необходимо и достаточно существование допустимого плана для каждой из них.
Теорема (первая теорема двойственности). Если одна из двойственных задач имеет оптимальное решение, то и другая имеет оптимальное решение, причем экстремальные значения целевых функций равны: 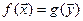. Если одна из двойственных задач неразрешима вследствие неограниченности целевой функции на множестве допустимых решений, то система ограничений другой задачи противоречива.
Экономическое содержание первой теоремы двойственности состоит в следующем: если задача определения оптимального плана, максимизирующего выпуск продукции, разрешима, то разрешима и задача определения оценок ресурсов. Причем цена продукции, полученной при реализации оптимального плана, совпадает с суммарной оценкой ресурсов. Совпадение значений целевых функций для соответствующих планов пары двойственных задач достаточно для того, чтобы эти планы были оптимальными. Это значит, что план производства и вектор оценок ресурсов являются оптимальными тогда и только тогда, когда цена произведенной продукции и суммарная оценка ресурсов совпадают. Оценки выступают как инструмент балансирования затрат и результатов. Двойственные оценки, обладают тем свойством, что они гарантируют рентабельность оптимального плана, т. е. равенство общей оценки продукции и ресурсов, и обусловливают убыточность всякого другого плана, отличного от оптимального. Двойственные оценки позволяют сопоставить и сбалансировать затраты и результаты системы.