Главная | Обратная связь

Алгоритм нахождения решения ДЗЛП по решению ЗЛП

1. Составляется симплекс-таблица для прямой ЗЛП. Фиксируется первичный набор базисных переменных.

2. Решается прямая ЗЛП.

3. На основе последней итерационной симплекс-таблицы формируется так называемая «обратная матрица»: она составляется из столбцов, которые соответствуют переменным из первичного базисного набора.

4. Фиксируется последний базисный набор.

5. Формируется коэффициентная строка: строго в том порядке, в каком стоят переменные в последнем базисном наборе, в коэффициентную строку переносятся коэффициенты целевой функции при этих переменных.

6. Решение ДЗЛП есть произведение коэффициентной строки и обратной матрицы.

Теорема (о дополняющей нежесткости, вторая теорема двойственности).Для того, чтобы планы 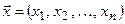и 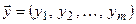пары двойственных задач были оптимальны, необходимо и достаточно выполнение условий:

,

,

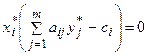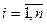
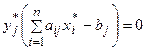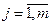
Эти условия называются условиями дополняющей нежесткости. Из них следует: если какое-либо ограничение одной из задач ее оптимальным планом обращается в строгое неравенство, то соответствующая компонента оптимального плана двойственной задачи должна равняться нулю; если же какая-либо компонента оптимального плана одной из задач положительна, то соответствующее ограничение в двойственной задаче ее оптимальным планом должно обращаться в строгое равенство.

Экономически это означает, что если по некоторому оптимальному плану производства расход i-го ресурса строго меньше его запаса 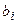, то в оптимальном плане соответствующая двойственная оценка единицы этого ресурса равна нулю. Если же в некотором оптимальном плане оценок его i-й компонент строго больше нуля, то в оптимальном плане производства расход соответствующего ресурса равен его запасу. Отсюда следует вывод: двойственные оценки могут служить мерой дефицитности ресурсов. Дефицитный ресурс (полностью используемый по оптимальному плану производства) имеет положительную оценку, а ресурс избыточный (используемый не полностью) имеет нулевую оценку.

Теорема (об оценках). Двойственные оценки показывают приращение функции цели, вызванное малым изменением свободного члена соответствующего ограничения задачи математического программирования, точнее