 |
|
Двойственные задачи ЛП.
Каждой задаче линейного программирования можно определенным образом сопоставить некоторую другую задачу линейного программирования, называемую двойственной или сопряженной по отношению к исходной или прямой. Связь исходной и двойственной задач заключается главным образом в том, что решение одной из них может быть получено непосредственно из решения другой.
Пример.
Прямая задача:
Сколько продукции и какого вида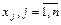 
необходимо произвести предприятию, чтобы при заданных стоимостях 
единицы продукции, объемах имеющихся ресурсов 
и нормах затрат каждого ресурса на единицу каждого вида продукции 
, максимизировать выпуск продукции в стоимостном выражении?
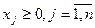
Двойственная задача:
Какие цены 
на единицу каждого из видов ресурсов нужно назначить при заданных их количествах 
и величинах стоимости выпускаемой из этих ресурсов продукции , а также нормах затрат каждого ресурса на единицу каждого вида продукции , чтобы продать ресурсы было бы не менее выгодно, чем производить продукцию?
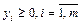
На основавнии этого примера построена пара симметричных двойственных задач. В матричной форме записи она выглядит следующим образом:
| 
|
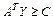
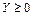
Если поменять местами прямую и двойственную задачи, то будет получена еще одна пара симметричных двойственных задач:
| 
|
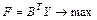
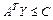
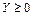
Из анализа записи симметричных двойственных задач могут быть сформулированы правила их построения:
1. Каждому i-му ограничению исходной задачи соответствует переменная 
двойственной задачи и, наоборот, каждому j-му ограничению двойственной задачи соответствует переменная 
исходной задачи. Т.е. число неравенств в системе ограничений одной задачи совпадает с числом переменных в другой задаче.
| 
|
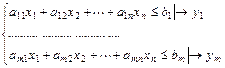
2. Матрицы коэффициентов систем ограничений исходной и двойственной задач являются взаимно транспонированными:
,
3. Свободные члены ограничений одной из задач являются коэффициентами при соответствующих переменных в целевой функции другой задачи.
4. В каждой задаче система ограничений задается в виде неравенств, причем в задаче, в которой ищется максимум целевой функции, все неравенства имеют вид «£», а в задаче, в которой находится минимум целевой функции, все неравенства имеют вид «³».
5. Максимизация целевой функции меняется на минимизацию, и наоборот.
6. Условия неотрицательности переменных сохраняются в обоих симметричных задачах.
Помимо симметричных пар двойственных задач существуют несимметричные пары двойственных задач. В матричной форме они имеею вид:
|
|
|
|
|
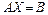
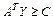
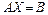
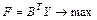
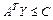
Для построения несимметричных пар двойственных задач добавляется правило:
Каждому ограничению-неравенству исходной задачи соответствует в двойственной задаче условие неотрицательности, а равенству – переменная без ограничения на знак. Наоборот, неотрицательной переменной соответствует в двойственной задаче ограничение - неравенство, а произвольной переменной – равенство.
Замечание. Если исходная задача линейного программирования записана в произвольной форме, то для записи двойственной задачи следует сначала записать исходную задачу в канонической или стандартной форме, а затем выписывать двойственную задачу.
Пример.
Исходная задача
Приведем все неравенства системы ограничений исходной задачи к одному знаку, в соответствии с тем, что целевая функция исследуется на min этот знак должен быть «³»:
Каждому неравенству будет соответствовать двойственная перемменная 
:
Тогда ограничения двойственной задачи будут иметь вид:
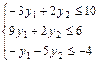
Функция цели двойственной задачи есть:
Если число переменных в исходной и двойственной задачах, образующих пару, равно двум, то, используя геометрическую интерпретацию задачи ЛП, можно легко найти решение данной пары задач.
При этом возможны три случая:
1) обе задачи имеют решение;
2) решение имеет одна задача;
3) обе задачи не имеют решения.
Пример.
Исходная задача Двойственная задача
Z = 2х1+7х2®max ` F = 14у1+8у2®min
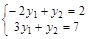
Пример.
Исходная задача Двойственная задача
L = 2х1+7х2®min `L = -14у1-8у2®max
Пример.
Исходная задача Двойственная задача
L = -2х1-3х2®min `L = 4у1+6у2®max
Исходная задача не имеет оптимального решения из-за неограниченности снизу ее целевой функции на множестве допустимых решений, тогда двойственная к ней задача вообще не имеет решения.