Главная | Обратная связь

Двойственный симплекс метод.

Теория двойственности позволяет усовершенствовать симплекс-метод и создать «улучшенный» симплекс-метод, который дает возможность получать сразу решение и исходной и двойственной задач. Такой метод называется двойственным симплекс методом. При его использовании можно выбирать для решения любую из пары двойственных задач, исходя из того какая из них проще.

Замечание. Так как объем вычислений в задаче ЛП связан в большей степени с количеством ограничений, чем с количеством переменных, то целесообразно переходить к решению двойственной задачи в том случае, когда ограничений больше, чем переменных.

Замечание. Двойственный симплекс-метод позволяет решать задачи линейного программирования, системы ограничений которых содержат свободные члены любого знака (при решении задач обычным симплексным методом эти числа предполагались неотрицательными).

 

Ввиду того, что двойственный симплекс-метод позволяет решать задачу с отрицательными правыми частями системы ограничений, то решение записанное на первой итерации является недопустимым. Соответствующий такому случаю план называется псевдопланом.

Идея двойственного симплекс-метода состоит в последовательном переходе от недопустимого решения к оптимальному. Алгоритм метода обеспечивает систематическое «приближение» решения к области допустимых решений. Тогда, когда полученное решение становиться допустимым, итерационный процесс заканчивается, так как это решение и является оптимальным.

Таким образом, как и обычный симплексный метод, двойственный симплекс-метод основан на использовании условий допустимости и оптимальности.

 

В основе алгоритма двойственного симплекс метода лежат теоремы.

Теорема 1.Если в псевдоплане , определяемом базисом , есть хотя бы одно отрицательное число такое, что все сответствующие ему , то задача вообще не имеет планов.

Теорема 2. Если в псевдоплане , определяемом базисом , имеются отрицательные числа такие, что для любого из них существуют числа , то можно перейти к новому псевдоплану, при котором значение целевой функции задачи улучшится.

 

Сформулируем алгоритм двойственного симплекс-метода.

Этап 1. Построение начального псевдоплана задачи.

Этап 2. Проверка псевдоплана на оптимальность.

Если все базисные переменные неотрицательные, то полученное решение - допустимое и оптимальное. В противном случае либо устанавливают неразрешимость задачи, либо переходят к новому псевдоплану.

Этап 3. Определение исключаемой и включаемой в базис переменных.

В качестве исключаемой из базиса переменной выбирается наибольшая по абсолютной величине отрицательная базисная переменная (при наличии альтернатив выбор делается произвольно), определяющая ключевую строку. Если все базисные переменные неотрицательные, процесс вычислений заканчивается, так как полученное решение допустимое и оптимальное.

Включаемая в базис переменная выбирается из числа небазисных переменных следующим образом. Вычисляются отношения оценок к соответствующим отрицательным коэффициентам ключевой строки, ассоциированной с исключаемой переменной (отношения с положительным или нулевым значением знаменателя не учитываются). В задаче минимизации вводимой в базис переменной должно соответствовать наименьшее из указанных отношений, а в задаче максимизации – отношение, наименьшее по абсолютной величине (при наличии альтернатив выбор делается произвольно). Если при этом знаменатели всех отношений равны нулю или положительные, задача не имеет допустимых решений.

Этап 4. Пстроение нового плана.

После выбора включаемой в базис и исключаемой из базиса переменных для получения следующего плана осуществляется обычная операция преобразования строк симплексной таблицы.

Затем повторяются действия начиная с этапа 2.

Пример.

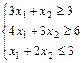
Перепишем задачу в виде:

Перейдем к канонической форме:

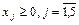
Двойственная ей несимметричная задача будет иметь вид:

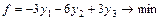
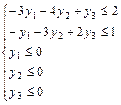
Начальная симплекс-таблица, записанная для прямой задачи, имеет вид:

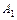
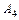
		-3	-3	-1
		-6	-4	-3
	-2	-1
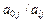
	1/2	1/3

 

Из таблицы видно, что в строках записана прямая задача, а в столбцах записана двойственная задача.

Начальный псевдоплан является недопустимым. Поэтому необходимо продолжить итерационный процесс.

На данной итерации исключаемой из базиса переменной является 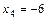. Минимальное отношение min( 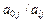)=1/3 соответствует переменной 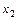, которая войдет в базис.

Пересчитанная симплекс таблица будет иметь вид:

		B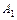
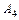
		-1	-5/3			-1/3
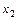
			4/3			-1/3
		-1	-5/3			2/3
		4/3			1/3
	-2/3			-1/3
	2/5

 

Новый псевдоплан также является недопустимым. Поэтому необходимо продолжить итерационный процесс.

На данной итерации исключаемыми из базиса переменными могут быть переменные и 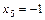, выберем . Минимальное отношение min( 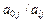)=2/5 соответствует переменной , которая войдет в базис.

Пересчитанная симплекс таблица будет иметь вид:

		B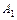
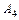
		3/5			-3/5	1/5
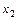
		6/5			4/5	-3/5
					-1
	12/5			-2/5	-1/5
			-2/5	-1/5

 

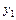
Полученный псевдоплан является допустимым, а значит и оптимальным. Поэтому решение задачи есть:

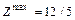в точке .

В симплексной таблице, соответствующей оптимальному решению прямой задачи, можно найти и оптимальное решение двойственной задачи.

Для этого устанавливается взаимнооднозначное соответствие между переменными прямой и двойственной задач. Исходным переменным прямой задачи ставятся в соответствие балансовые (дополнительные) переменные двойственной, а балансовым (дополнительным) переменным прямой задачи ставятся в соответствие исходные переменные двойственной задачи:

Оптимальное решение двойственной задачи определяется коэффициентами строки оценок в оптимальной симплексной таблице.

Переменные двойственной задачи приравниваются к коэффициентам при соответствующих им небазисных переменным в строке оценок оптимальной симплекс-таблицы прямой задачи. Остальные переменные равны нулю.

 

Поэтому для рассматриваемого примера оптимальное решение двойственной задачи есть:

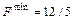в точке .