Главная | Обратная связь

Вопрос 9. Движение электронов в аксиально–симметричном неоднородном магнитном поле. Короткая магнитная линза.

Пускай наше магнитное поле не зависит от поворота угла φ. Здесь мы рассматриваем цилиндрическую систему координат. Пускай налетает частица (электрон) . У такой системы будет компонента по φ, так как частица, при попадании в магнитное поле начнет закручиваться.

Векторное поле можно описать при помощи векторного потенциала: 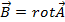. У векторного потенциала будет только угловая составляющая (следует из rot в явном виде в полярных координатах). A_φ=A(r,z), от φ не может зависеть из-за симметрии.

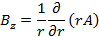
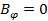
Запишем формулу Лагранжа:

Расписав импульс и силу через формулу Лагранжа, получим:

1)

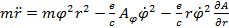
2)

3) (это момент импульса на ось z – интеграл движения)

Вместо А подставляем поле:

1)

2)

3)

Из всего этого получаем:

Требуется найти r(z).

Так как и B_r и B_φ связаны, то

Следовательно получим:

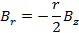
Предположение: пусть наш пучок параллелен (сильное предположение), тогда считаем, что 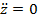, так как r мало, то r² малая величина второго порядка, следовательно v_z=const. То есть 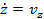. Тогда из формулы найдем . Теперь, расписывая вторую производную по времени от r имеем:

Это и есть уравнение траектории. Соответственно, если посчитать, подставив, нужные описанные здесь отношения в дифференциальное уравнение по углу φ, то получим для него формулу. Упуская эти математические преобразования, дается результат:

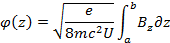
Таким образом, была получена система уравнений траектории частицы в аксиально-симметричном неоднородном поле.

 

Электромагнитные линзы позволяют получить поля большой силы, но обеспечить стабильность электрического тока, питающего катушку, очень сложно. Круглая катушка (соленоид), через которую течет ток, создает магнитное поле с круговой симметрией. Различают длинные и короткие линзы. Электроны в магнитном поле катушки описывают винтовые траектории, и проекции этих траекторий на плоскость, перпендикулярную магнитному полю, являются окружностью, если электроны имеют радиальную составляющую скорости. Если электроны движутся параллельно оси, они не подвергаются действию поля. Вследствие однородности поля магнитной катушки траектории электрона полностью проходят внутри катушки, поэтому можно получить изображения только в масштабе 1:1.

Увеличение или уменьшение изображения достигается лишь в коротких линзах, в которых электронный луч подвергается воздействию магнитного поля на коротком отрезке своего пути. Длина катушки меньше ее диаметра (см.рис.). Круглое кольцо, состоящее из нескольких витков провода, действует как короткая магнитная линза.

Электроны, вылетающие из точки О со скоростью v под углом a к оси магнитной линзы, сначала, находясь вне поля, движутся прямолинейно. Затем, по мере захода в область действия линзы, электроны начинают подвергаться воздействию силы F, направленной перпендикулярно H и v. В результате такого воздействия электрон приобретает вращательную составляющую скорости v в. Взаимодействие магнитного поля H пр с составляющей v в приводит к появлению силы, направленной к оси и создающей фокусировку.

Вследствие винтообразной формы траектории создается поворот изображения. Для его компенсации применяют вторую катушку с обратным знаком поля.

№10.

11 вопрос. Ограничение тока пространственным зарядом. Вывод формулы Чайльда-Ленгмюра для плоских электродов. Имеется плоский конденсатор. Между его обкладками подается напряжение. Самое очевидное, что приходит в голову, что между обкладками конденсатора создается линейно возрастающий потенциал от 0 до Ua, где Ua – потенциал на аноде. Это верно лишь в том случае, если между катодом и анодом нет пространственного заряда. Чтобы объяснить какой потенциал будет между обкладками конденсатора, возьмем некоторые предположения: 1) V=0 скорость вылетевших с катода электронов. 2) Бесконечно большая эмиссионная способность I<<Iнасыщения. 3) 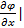x=0=0 Если бы >0 => все электроны бы долетели до анода, если <0 => то не долетели бы. Имеем для пространственного заряда уравнение Пуассона: Или же 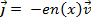Переписывая уравнение Пуассона, выразив n(x) через j, и v. А v найдя из следующего уравнения 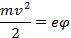Получаем: После небольшого финта ушами и некоторых математических преобразований (упускаю из-за небольшой громоздкости и не имеющего к краткой сути дела отношения) переходим к ответу: Переходя от потенциала к плотности тока и подставляя граничное условие для потенциала ( ) получим формулу Чайльда-Ленгмюра. Эта формула справедлива при: 1) ток I<Iн 2) We << U Аналогично размышляя можно вывести эту формулу для цилиндрического случая. Немного подробнее: Второй член в сумме будет равен 0 (?). Но в конечном итоге получим: Где ra – радиус анода, l – высота цилиндра, r0 – радиус катода. Если у нас We сравнимо с U, то появляется «прогиб» потенциала между обкладками конденсатора, и самая нижняя точка в яме называется виртуальным катодом. 12ФОКУСИРОВКА ПАРАКСИАЛЬНОГО ПУЧКА ЗАРЯЖЕННЫХ ЧАСТИЦ В МАГНИТНОМ ПОЛЕ.

Рассмотрим движения заряда, влетающего с некоторой скоростью v << c в однородное магнитное поле, индукция которого перпендикулярна направлению скорости. На движущийся заряд действует сила Лоренца, равная в гауссовой системе единиц F_л = (q/c)[vB]. Эта сила перпендикулярна направлению движения заряда и не изменяет поэтому абсолютное значение его скорости. Траектория движения заряда представляет собой в этих условиях окружность. Радиус этой окружности можно найти приравняв силу Лоренца к центростремительной силе F_л = mV²/R. Отсюда получаем R = mcV/qB. Угловая частота вращения вокруг направления поля называется циклотронной частотой и равна ω = V/R = qB/mc.

Вдоль направления магнитного поля никаких сил на заряженную частицу не действует. Если частица имела проекцию скорости на направление магнитного поля, то она будет продолжать двигаться в этом направлении с неизменной начальной скоростью. Поэтому в общем случае траектория движения частицы представляет собой винтовую линию. Скорость заряда можно разложить на составляющую вдоль поля V_B=V·cosα и на составляющую, перпендикулярную магнитному полю V_T=V·sinα, где α - угол между направлением скорости и направлением магнитного поля. Найдём расстояние, которое проходит заряд в направлении вдоль поля за один оборот винтовой линии T = 2π/ω = 2πmc/qB. За это время заряд проходит вдоль магнитного поля расстояние L = V_BT = 2πc·Vcosα/(q/m)B. Если апертура пучка заряженных частиц мала, то cosα ≈ 1 и L ≈ 2πcV/(q/m)B.

Таким образом, расстояние L, проходимое зарядами вдоль поля за один оборот, не зависит от угла α и все заряды, вышедшие из одной точки под разными малыми углами, после одного оборота вновь соберутся в точке (сфокусируются). Расстояние от источника заряженных частиц до точки их фокусировки может быть использовано для экспериментального определения отношения заряда частицы к её массе.