 |
|
Линейные системы векторов
Бинарные отношения
- Установить свойства и начертить график бинарного отношения R={(x,y)ÎR2çxy>1Ùx>0}.
- Задано бинарное отношение R={(x,y)ÎR2çxy=1Ùx=y}. Указать верные и неверные утверждения.
а) Отношение R рефлексивное, так как истинно высказывание: "xÎR (x2=1Ùx=x).
б) Данное бинарное отношение не рефлексивное, так как не для всякого действительного числа его квадрат равен 1.
в) Отношение R симметричное, так как истинно высказывание: "x,yÎR((xy=1Ùx=y)Þ(yx=1Ùy=x)).
г) Данное бинарное отношение не симметричное, так как из равенства xy=1 не следует равенство y=x.
d) Данное бинарное отношение транзитивно, т.к. истинно высказывание: ( " x,y,zÎR ) (( xy = 1 )Ú( x = y )) Ù (( yz = 1)Ú( y = z )) ® (( xz = 1 )Ú( x = z )).
е) Данное бинарное отношение не транзитивно, т.к. из равенства xy = 1 и yz = 1 не следует равенство xz = 1. Например, x = 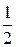 , y = 2 , z =
, y = 2 , z = 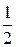 и xz =
и xz = 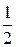
 =
=  .
.
ж) Данное бинарное отношение является отношением эквивалентности и разбивает множество R на классы { 0 }, { 1 }, {–1 },...,{ 2, 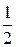 }, {–2, –
}, {–2, – 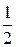 },..., { a,
},..., { a,  }, {–a, –
}, {–a, –  }, ... , где aÎR , a ¹ 0.
}, ... , где aÎR , a ¹ 0.
з) Данное бинарное отношение не рефлексивно, не симметрично, не транзитивно. Следовательно, не является отношением эквивалентности.
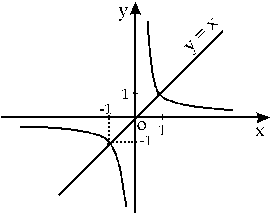
и) График гиперболы  ( xy = 1 ) и точка О( 0,0 ) ( т.к. 0 = 0 ) являются графиком бинарного отношения R
( xy = 1 ) и точка О( 0,0 ) ( т.к. 0 = 0 ) являются графиком бинарного отношения R

к) График гиперболы  ( xy = 1 ) и прямой y = x ( x = y ) в объединении дают график бинарного отношения R
( xy = 1 ) и прямой y = x ( x = y ) в объединении дают график бинарного отношения R
Доказать методом математической индукции:
- n(n2 + 5 )
 6, где nÎN, n ³ 1.
6, где nÎN, n ³ 1. - 13 + 23 + 33 +¼+ n3 = (1 + 2 + 3 +¼+ n)2, где nÎN,n ³ 1.
Комплексные числа
- Вычислить: (2+3i)(4–5i) + (2–3i)(4+5i).
- Найти х и у, считая их действительными числами:
(1+2i)x + (3–5i)y = 1–3i
- При каких условиях произведение двух комплексных чисел является действительным числом?
- Вычислить, пользуясь формулой Муавра:
 .
.
- Извлечь все корни:
1)  . 2)
. 2)  . 3)
. 3) 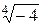 . 4)
. 4)  . 5)
. 5)  .
.
- Выполнить действия:
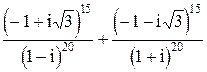 .
.
Системы линейных уравнений
- Решить систему линейных уравнений методом последовательного исключения переменных:
1)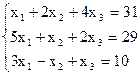 2)
2) 
3) 4)
4) 
5)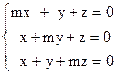 6)
6) 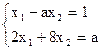 .
.
Линейные системы векторов
12. Доказать, что при любых a, b и g система векторов  ,
, 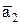 ,
, 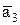 линейно независима, если
линейно независима, если  =( 1, a, b ),
=( 1, a, b ), 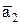 =( 0, 1, g ),
=( 0, 1, g ), 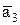 =( 0, 0, 1 ).
=( 0, 0, 1 ).
13. Исследовать, является ли R подпространством векторного пространства C над полем F, если: 1)F = R; 2)F = C; 3)F = Q.
14. Исследовать, является ли линейно зависимой система векторов  :
:
1) 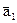 =(1, 2, 1), 2)
=(1, 2, 1), 2) 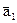 =(1,–2,–1),
=(1,–2,–1),
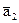 =(1, 1,–1),
=(1, 1,–1), 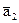 =(–1, 1,–1),
=(–1, 1,–1),
 =(–1,–3,–3).
=(–1,–3,–3).  =(–1,–3,–3).
=(–1,–3,–3).
- Исследовать, является ли линейно зависимой система векторов
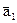 ,
, 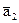 векторного пространства многочленов от одной переменной степени £ 2 над полем R, если
векторного пространства многочленов от одной переменной степени £ 2 над полем R, если
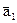 =f1(x)=3+x+2x2,
=f1(x)=3+x+2x2, 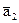 =f2(x)=–2+x–x2.
=f2(x)=–2+x–x2. - Доказать, что в вещественном пространстве квадратных матрицах второго порядка первый из трех векторов
 ,
,  ,
,  не выражается линейно через остальные.
не выражается линейно через остальные. - Исследовать, является ли линейно зависимой система векторов
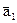 ,
, 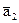 векторного пространства C над R, если
векторного пространства C над R, если 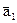 =2+5i,
=2+5i, 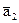 =4+10i.
=4+10i. - Верно ли, что в вещественном пространстве многочленов степени = 2 вектор f(x) = 1 + 4x – 7x2 линейно выражается через векторы f1(x) = 2 – x + x2, и f2(x) = 1 – 2x + 3x2.
- Подпространство V0 натянуто на систему векторов
 , где
, где
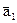 =(1, 2, 1),
=(1, 2, 1), 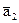 =(1, 1,–1),
=(1, 1,–1),  =(1, 3, 3). Найти базис и размерность V0.
=(1, 3, 3). Найти базис и размерность V0. - Решить векторное уравнение:
 , где
, где
 ,
,  ,
,  ,
, 
- Вычислить ранг матрицы

