 |
|
Полиномы от одной переменной
⇐ ПредыдущаяСтр 2 из 2
- Найти сумму f(x) и g(x), если
f(x)=2x6+3x5–8x3+17x2–35x–18, g(x)=–2x6+5x5–2x4+10x3+35x+8. - Найти произведение fg в кольце Z6[x], если f=2x3–3x2–5x+4, g=3x3+5x2–4x+3.
- Найти необходимое и достаточное условия делимости многочлена f(x) на j(x), если f(x)=x3+2x2+ax–3, j(x)=x2–px+q.
- Найти частное a и остаток r, если f=2x5+3x4–6x3–5x+7, g=x3+2x2–3x+1, f=g·q+r.
- Выполнить деление с остатком f на g в кольце многочленов над кольцом классов вычетов Z3[x] по модулю 3, если f=2x4+x+1, g=2x+1.
- Разложить многочлен f(x)=x12–2x6+1 на неприводимые множители над полем действительных чисел.
- Найти необходимое и достаточное условия делимости многочлена f(x) на j(x), если f(x)=x3+2x2+ax–3, j(x)=x2–px+q.
- Выполнить деление с остатком в Q[x] f на g:
f=x6–7x5–13x 4+4x2+11x–5, g=x3–5x2+4x–3.
- Найти необходимые и достаточные условия делимости f на g: f=x3+ax2+3x+c, g=x2+px+2.
- Найти необходимые и достаточные условия делимости первого многочлена на второй: f=x3+px+q, g=x2+mx–1.
- Найти остаток от деления f на g, пользуясь схемой Горнера: f=x4–2x3+4x2–6x+8, g=x–1.
Наибольший общий делитель и наименьшее общее кратное двух полиномов
- Найти НОД и НОК:
f1=x3+2x2+3x +2, f2=x4+x3+x2–x–2, f3=x3–x2–4. - Найти НОД многочленов f(x) и g(x):
1) f(x)=x6+x5–3x4+2x3+4x–2, g(x)=x5+3x4+x3+6x2+4x+6.
2) f(x)=(x–1)813(x+2)107(x–3)91 , g(x)=x9+x8–5x7+x6+11x5–13x4–7x3+15x2–4. - Для многочленов f=x3–x2+3x–10 и g=x3+6x2–9x–14 найти такие многочлены u и v, что f·u+g·v=d, где d=НОД(f,g).
- Найти НОД(f,g) и его линейное представление через f и g: f=x3–1, g=x4+x3+2x2+x+1.
- Найти НОК(f,g): f=x33–1, g=x18–1.
- Найти НОД и НОК: f=x4–4x3+1, g=x3–3x2+1.
Корни многочлена и схема Горнера
- С помощью схемы Горнера найти неполное частное и остаток от деления f на g, если f=8x8–10x7+36x6–28x5+4x3–24x2+20x+11, g=4x+3.

- Найти кратность корня c = –2 у многочлена f, если f=x5+6x4+11x3+2x2–12x–8.
- Разложить f по степеням двучлена x+2, если f=3x5+7x4+x3–2x+3.
- Записать в стандартном виде многочлен f: f=(x+2)5–3(x–2)3.
Полиномы над числовыми полями
- Доказать неприводимость над Q полинома f: f=x4–2x+3.
- Разложить многочлен f(x)=x12–2x6+1 на неприводимые множители над полем действительных чисел.
- Найти многочлен с действительными коэффициентами наименьшей степени, который имеет своими конями числа 2+i, 3 и двукратный корень 1+i.
- При каком l многочлены f=x3–2lx+l3 и g=x3+l2–2 имеют общий корень в C?
Симметрические полиномы
- Выразить симметрический многочлен через элементарные симметрические многочлены:
а) f(x1,x2,x3)=x13+x22+x33+3x1x2x3 б) f(x1,x2,x3)=x12+x22+x32+2x1+2x2+2x3.
- Многочлен f представить как многочлен от x3 над кольцом R[x1,x2], если f=4x13x2x32+3x1x22x32–x12x2x33+2x1x22x3–3x13x22x3+2x13x33+8x1x3–5x1x2+2x3–17.
Теория делимости
- Вычислить НОД(588, 2058, 2849) двумя способами.
- Вычислить НОД(99, 162) и выразить его через данные числа.
- Найти натуральное число, зная, что оно имеет два простых делителя, всего 6 натуральных делителей, сумма которых равна 28.
- Найти натуральное число, произведение всех натуральных делителей которого равно 5832.
- Найти количество натуральных чисел, не превосходящих 100 и не делящихся ни на одно из простых чисел: 5, 7, 11.
- Решить в натуральных числах системы уравнений:
а)  , б)
, б)  .
.
- Построить графики функций:
а) y=j (x), б) y=t(x), в) y= s(x), где x Î N.
Теория сравнений
- По какому модулю числа 20,–4, 22, 18,–1 составляют полную систему вычетов?
- Доказать, что система чисел 20, 31,–8, –5, 25, 14, 8,–1, 13, 6 не являются полной системой вычетов по модулю 10.
- Почему система чисел –5, 13, 11,–25, 5 не является приведенной системой вычетов по модулю 12?
- Решить сравнения:
1) 3xº4(mod 5), 2) 12xº16(mod 20), 3)12xº15(mod 20). - Вычислить последние две цифры числа 2102.
- Дробь
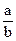 - несократима. Будет ли несократимой дробь
- несократима. Будет ли несократимой дробь 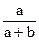 ?
? - Представить в виде систематической записи: (51306)7.
- Перейти к двоичной системе счисления:
n=46=(46)10.
- Перейти к 12-ричной системе счисления: n=19510.
- Исследовать применяя признаки делимости, делится ли число А на а, если:
1) А=61907531, а=7.
2) А=65204779728, а=3256.
Основные понятия теории групп
- Доказать, что множество целых чисел, кратных 3, есть подгруппа аддитивной группы целых чисел.
- Доказать, что множество матриц вида
 , где аÎR \ {0}, есть подгруппа мультипликативной группы G всех невырожденных матриц второго порядка.
, где аÎR \ {0}, есть подгруппа мультипликативной группы G всех невырожденных матриц второго порядка. - Исследовать, образует ли группу относительно операции умножения чисел множество М, где М={1,–1, i,–i }, i-мнимая единица.
- Пусть G- мультипликативная группа невырожденных матриц второго порядка. Найти порядки элементов a1 , a2ÎG, если
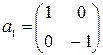 ,
,  .
. - Доказать, что отображение x ® 3x является изоморфизмом аддитивной группы действительных чисел на мультипликативную группу положительных действительных чисел.
- Доказать, что аддитивную группу всех функций вида ax + b (a, b ÎR ) можно гомоморфно отобразить на аддитивную группу R,и найти ядро этого гомоморфизма
- Пусть все элементы группы, кроме единицы, имеют порядок 2. Доказать, что группа абелева.
Кольца и поля
- Исследовать, образует ли кольцо относительно операций сложения и умножения матриц множество М матриц вида
 , где a, b- любые действительные числа.
, где a, b- любые действительные числа. - Исследовать, образует ли кольцо относительно обычных операций сложения и умножения множество Z[i] комплексных чисел вида x+yi, где x,yÎZ.
- Пусть на множестве R задано обычное сложение, а умножение Ä: aÄb=b для любых a, bÎR. Показать, что R не является кольцом относительно (+) и Ä.
- Пусть


Доказать, что К - кольцо относительно Å и Ä.
- Составить таблицу Å и Ä элементов колец вычетов а) Z 3, б) Z 8 и выяснить, имеются ли в этих кольцах делители нуля.
- Проверить, образует ли поле кольцо <A,+,•> , если
A= .
. - Проверить, отображение j, такое, что
j: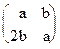 →
→ 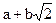 , является ли изоморфизмом поля F1 на поле F2, где F1=
, является ли изоморфизмом поля F1 на поле F2, где F1= 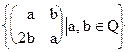 , F2=Q(
, F2=Q( 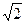 )=
)= 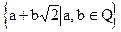 , а операции определены как обычно.
, а операции определены как обычно.
©2015 arhivinfo.ru Все права принадлежат авторам размещенных материалов.