Главная | Обратная связь

Тригонометрические ряды. Задача о разложении функции в

ТригонометрическиЕ ряды

В естествознании и технике часто приходится иметь дело с периодическими процессами: колебательными и вращательными движением различных деталей машин и приборов, периодическим движением небесных тел и элементарных частиц, акустическими и электромагнитными колебаниями.

В математике все такие процессы описываются периодическими функциями. Простейшими периодическими функциями являются, как известно, тригонометрические функции sin(t) и cos(t). Одним из главных вопросов изучаемой темы является вопрос о представлении произвольной функции суммой гармонических функций (гармоник). В данной лекции начнем с рассмотрения общих вопросов, подробно изучим важнейшую для многих практических задач так называемую тригонометрическую систему функций и получающийся на ее основе тригонометрический ряд.

Тригонометрические ряды. Задача о разложении функции в

Напомним, что функция f(t) одной переменной t называется периодичной, если существует такое число Т ¹ 0, называемое ее периодом, что

f(t + Т) = f(t) при всех значениях t ( –¥ < t < + ¥).

Простейшими периодическими функциями являются, как известно, тригонометрические функции sin t и cos t с периодом Т = 2p.

В физике простейшей периодической функцией обычно считают "гармонику" (или "гармоническое колебание")

g(t) = A sin(wt + j), –¥ < t < + ¥.

Так как g(t + ) = g(t), при –¥ < t < + ¥, то Т = есть период гармоники. Константы А, w и j называют соответственно амплитудой, частотой и фазой гармоники.

Одним из основных вопросов данной лекции является вопрос о представлении произвольной периодической функции в виде суммы гармоник.

Рассмотрим последовательность гармоник

k = 1, 2, …, –¥ < t < + ¥ (1)

Частотой k-й гармоники является 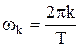k = 1, 2, … .

Таким образом, частоты гармоник последовательности (1) являются кратными одному и тому же числу 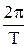. Такие гармоники мы будем называть гармониками с кратными частотами. Частота w = 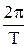называется основной частотой. Рассмотрим последовательность гармоник, для которых основная частота w = 1. Это можно сделать, не умаляя общности рассуждений, как будет показано ниже. Рассмотрим последовательность гармоник

k = 1, 2, … .

Сумма, или, как говорят, суперпозиция бесконечного числа таких гармоник, есть сумма сходящегося ряда

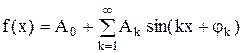(2)

Ясно, что эта сумма является периодической функцией с периодом

Т = 2p.

Равенство (2) можно преобразовать так.

Учтем, что

A_ksin (kx + j_k) = A_ksinj_k coskx + A_kcosj_k sinkx.

Обозначим 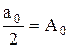, a_k = A_ksinj_k , b_k = A_kcosj_k.

Тогда равенство (2) примет вид

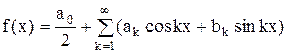. (3)

Определение. Ряд в правой части равенства (3) называется тригонометрическим рядом, а само равенство (3), если оно имеет место при всех х, – разложением функции f(x) в тригонометрический ряд.

Основной задачей данной темы является исследование вопросов:

1) Какую периодическую функцию с произвольным периодом можно разложить в тригонометрический ряд вида (3)?

2) Как найти коэффициенты разложения (3) а₀, а_k и b_k, если это разложение возможно?

3) Какова зависимость между характером сходимости ряда (3) и свойствами функции f(x)?