Главная | Обратная связь

Ряд Фурье для четных и нечетных функций

Формулы для коэффициентов Эйлера значительно упрощаются, если f(x) - четная или нечетная функция. Выведем сначала некоторые формулы, необходимые для дальнейших вычислений.

а) Пусть j(x) – четная функция на отрезке [–l; l], т. е. j(-х) = j(х).

Тогда .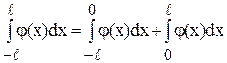

Сделав в первом интеграле правой части замену:

x = - t Þ dx = - dt; 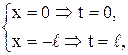получим:

.

б) Пусть j(x) – нечетная функция на отрезке [–l; l], т. е. j(-х) = – j(х).

Тогда

= (замена, как и в первом интеграле)

= .

Итак, для четных функций ,

для нечетных функций . (9)

Используем эти результаты при вычислении коэффициентов Фурье.

а) Для четных функций.

Пусть f(x) – четная функция на отрезке [–l, l].

Тогда – тоже четная функция, а 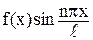– нечетная функция. Значит, используя (9), получим:

(10)

Таким образом, в разложении четных функций в ряд Фурье "останутся только косинусы":

f(–x) = f(x) Þ f(x) = .

б) Для нечетных функций.

Пусть f(x) – нечетная функция на отрезке [– ; ], тогда – тоже нечетная функция, а 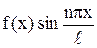– четная функция (как произведение двух нечетных функций). Значит, используя (10), получим:

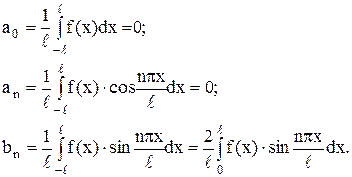(11)

Тогда в разложении нечетной функции в ряд Фурье "останутся только синусы":

f(–x) = – f(x) Þ f(x) = .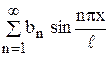

Примеры разложения

Пример 1. Разложить в ряд Фурье функцию f(x) = |x| на отрезке [–p; p].

Решение.

 

 

Так как |x| – четная функция, используем формулы (10):

b_n = 0, ,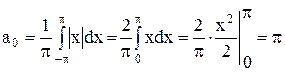

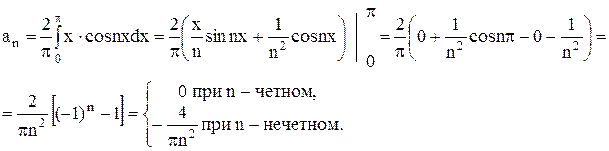
Тогда ряд Фурье примет вид или

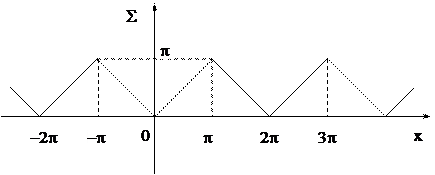. График ряда изображен на рис.

Пример 2. Разложить в ряд Фурье функцию, график которой имеет вид:

Решение.

Так как f(x) – нечетная функция, используем формулы (11):

,

.

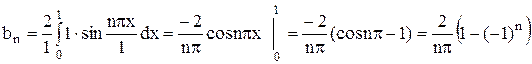Т.о., при четных n получим b_n = 0, а для нечетных n будем иметь:

.

Тогда ряд Фурье примет вид

.

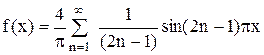Отметим еще раз, что равенство функции и полученного ряда выполняется только там, где f(x) непрерывна. В точках разрыва полученный ряд сходится к полусумме односторонних пределов, в данном случае к числу 0.