 |
|
Дифракция на решетке
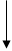 l
l
 d
d








 q
q
qD = d sin(q)
Разность хода:
D= d sin(q).
Условие главных минимумов:
d sin(q) = ml
Дополнительных минимумов:
d sin(q) =±(m¢/N)×l,
m¹ pN p = 0,1,2.. (m не кратно числу штрихов решетки)
Условие главных максимумов:
d sin(q) = ml, m£d/l.
Где d – постоянная решетки;
m- порядок спектра;
q - угол дифракции;
l - длина волны падающих лучей.
Постоянная решетки (период решетки):
d=1/N0,
N0=  - число щелей на единицу длины решетки.
- число щелей на единицу длины решетки.
Разрешающая способность дифракционной решетки
R =  =m N,
=m N,
где N – общее число щелей,
m – порядок спектра,
l и l + Dl -длины волн двух близких спектральных линий.
Угловая дисперсия дифракционной решетки характеризует степень
пространственного (углового) разделения волн с различными длинами:
D =  .
.
Единица измерения радиан на ангстрем ,  .
.
Линейная дисперсия дифракционной решетки:
D1 = f×D =  ,
,
где f – фокусное расстояние линзы, проецирующей спектр на экран.
Единица измерения миллиметр на ангстрем,  .
.
Поляризация.
Поляризованный свет представляет собой волны, вектор  в которых имеет упорядоченный характер ориентации в пространстве. В зависимости от характера упорядочения различают линейную, круговую, элиптическую поляризации.
в которых имеет упорядоченный характер ориентации в пространстве. В зависимости от характера упорядочения различают линейную, круговую, элиптическую поляризации.
Степень поляризации:
Р =  ,
,
где Iпол – интенсивность поляризованной составляющей,
I0 – полная интенсивность частично - поляризованного света:
I0 = Iмакс + Iмин.
Для линейной поляризации ее можно представить в виде:
Р = 
где Iмакс , Iмин – соответственно максимум и минимум интенсивности света, проходящего через анализатор.
Для линейно поляризованного света (Iпол = I0) степень поляризации Р=1, для естественного света (Iпол = 0) Р=0.
Закон Малюса:
 Р
Р
 Е0 I = I0 cos2(j),
Е0 I = I0 cos2(j),
 Е j где I0 – интенсивность падающего
Е j где I0 – интенсивность падающего
плоскополяризованного света.
j- угол между направлением вектора 
О и направлением пропускания анализатора.
Закон Брюстера:
 tg(qбр) = n2/n1
tg(qбр) = n2/n1

 qбр При падении света под углом Брюстера
qбр При падении света под углом Брюстера




 S n1 отраженный и преломленный лучи
S n1 отраженный и преломленный лучи
взаимно ортогональны, причем степень
поляризации отраженного луча = 1
n2
Формулы Френеля: при отражении и преломлении света на границе раздела двух диэлектриков имеют место формулы Френеля.
Для амплитуд
Отражение Преломление
 ^= -
^= - 
 1^ =
1^ =  ^
^ 
 çç=
çç=  çç
çç 
 1çç =
1çç =  çç
çç  .
.
Для интенсивностей
 ¢^=
¢^=  I1^ = I ^
I1^ = I ^ 
 çç=
çç= 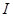 çç
çç  I1çç = Iôô
I1çç = Iôô  .
.