 |
|
Вероятностный подход к измерению дискретной и непрерывной информации
В основе теории информации лежит предложенный Шенноном способ измерения количества информации, содержащейся в одной случайной величине, относительно другой случайной величины, Этот способ приводит к выражению количества информации числом.
Для дискретных случайных величи 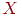 и
и  , заданных законами распределения
, заданных законами распределения  ,
,  и совместным распределением
и совместным распределением  , количество информации, содержащейся в
, количество информации, содержащейся в 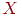 относительно
относительно  , равно
, равно

Для непрерывных случайных величин, 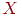 и
и  , заданных плотностями распределения вероятностей
, заданных плотностями распределения вероятностей 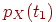 ,
,  и
и  , аналогичная формула имеет вид
, аналогичная формула имеет вид

Очевидно, что

и, следовательно,

Энтропия дискретной случайной величины 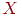 в теории информации определяется формулой
в теории информации определяется формулой

Свойства меры информации и энтропии:
-
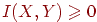 ,
,  и
и  независимы;
независимы; -
 ;
; -
 - константа;
- константа; -
 , где
, где  ;
; -
 . Если
. Если  , то
, то 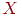 - функция от
- функция от  . Если
. Если 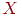 - инъективная функция1) от
- инъективная функция1) от  , то
, то  .
.
- Логарифмированием из очевидного для всех
 неравенства
неравенства  (равенство устанавливается только при
(равенство устанавливается только при  ) получается неравенство
) получается неравенство  или
или 


т.е.  только при
только при  для всех
для всех  и
и  , т.е. при независимости
, т.е. при независимости 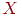 и
и  . Если
. Если 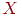 и
и  независимы, то
независимы, то  и, следовательно, аргументы логарифмов равны 1 и, следовательно, сами логарифмы равны 0, что означает, что
и, следовательно, аргументы логарифмов равны 1 и, следовательно, сами логарифмы равны 0, что означает, что  ;
;
- Следует из симметричности формул относительно аргументов;
- Если
 , то все члены суммы, определяющей
, то все члены суммы, определяющей  , должны быть нули, что возможно тогда и только тогда, когда
, должны быть нули, что возможно тогда и только тогда, когда 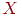 - константа;
- константа; - Из четырех очевидных соотношений



получается

- Нужно доказать
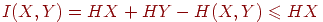 или
или  .
.

но  , а значит аргументы у всех логарифмов не больше 1 и, следовательно, значения логарифмов не больше 0, а это и значит, что вся сумма не больше 0.
, а значит аргументы у всех логарифмов не больше 1 и, следовательно, значения логарифмов не больше 0, а это и значит, что вся сумма не больше 0.
Если  , то для каждого
, то для каждого 
 равно либо
равно либо  , либо 0. Но из
, либо 0. Но из  следует
следует  , что возможно только в случае, когда
, что возможно только в случае, когда 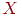 - функция от
- функция от  .
.
При независимости случайных величин, 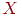 и
и  одна из них ничем не описывает другую, что и отражается в том, что для таких случайных величин,
одна из них ничем не описывает другую, что и отражается в том, что для таких случайных величин,  .
.
Рассмотрим пример измерения количества информации при подбрасывании двух игральных костей.
Пусть заданы дискретное случайные величины  ,
,  и
и  .
.  и
и  - количества очков, выпавших соответственно на 1-й и 2-й игральной кости, а
- количества очков, выпавших соответственно на 1-й и 2-й игральной кости, а  . Найти
. Найти  ,
,  ,
,  .
.
Законы распределения вероятностей для дискретной случайной величины  и
и  совпадают, т.к. кости одинаковые и без изъянов.
совпадают, т.к. кости одинаковые и без изъянов.

Закон распределения вероятностей для дискретной случайной величины  ,
,

вследствие того, что  ,
,  - независимы и поэтому
- независимы и поэтому

будет

Таблицы, определяющие  :
:


Закон совместного распределения вероятностей дискретной случайной величины  и
и  будет
будет

например,

 В общем случае получится
В общем случае получится


Тогда












Здесь  , что соответствует свойствам информации.
, что соответствует свойствам информации.
Подчеркнутый член  в расчете
в расчете  соответствует информации о двух случаях из 36, когда
соответствует информации о двух случаях из 36, когда  и
и  , которые однозначно определяют
, которые однозначно определяют  . Шесть случаев, когда
. Шесть случаев, когда 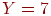 , не несут никакой информации об
, не несут никакой информации об  , что соответствует подчеркнутому члену
, что соответствует подчеркнутому члену  .
.
Расчеты можно проводить, используя 4-е свойство информации, через энтропию.


Расчет количества информации с использованием 4-го свойства, а не определения, обычно требует меньше вычислений.
Рассмотрим более простой пример. Пусть дискретная случайная величина 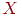 равна количеству очков, выпавших на игральной кости, а дискретная случайная величина
равна количеству очков, выпавших на игральной кости, а дискретная случайная величина  равна 0, если выпавшее количество очков нечетно, и 1, если выпавшее количество очков четно. Найти
равна 0, если выпавшее количество очков нечетно, и 1, если выпавшее количество очков четно. Найти  и
и  .
.
Составим законы распределения вероятностей дискретной случайной величины 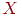 и
и  .
.

Таким образом, при 
 и, соответственно, при
и, соответственно, при 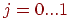
 .
.
Составим также закон совместного распределения вероятностей этих дискретных случайных величин

Таким образом,

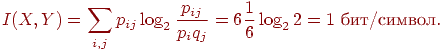

Точное количество выпавших очков дает точную информацию о четности, т.е. 1бит. Из  бит/сим и 3-го свойства информации следует, что информация об
бит/сим и 3-го свойства информации следует, что информация об 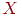 полностью определяет
полностью определяет  , но не наоборот, т.к.
, но не наоборот, т.к.  бит/сим. Действительно,
бит/сим. Действительно,  функционально зависит от
функционально зависит от 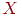 , а
, а 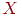 от
от  функционально не зависит.
функционально не зависит.
Расчеты через энтропию будут следующими
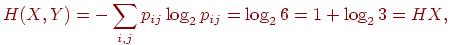

Упражнение 5 Найти энтропию дискретной случайной величины 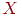 , заданной распределением
, заданной распределением

Упражнение 6 Значения дискретной случайной величины  и
и  определяются подбрасыванием двух идеальных монет, а дискретная случайная величина
определяются подбрасыванием двух идеальных монет, а дискретная случайная величина  равна сумме количества "гербов", выпавших при подбрасывании этих монет. Сколько информации об
равна сумме количества "гербов", выпавших при подбрасывании этих монет. Сколько информации об  содержится в
содержится в  ?
?
Упражнение 7 Сколько информации об  содержится в дискретной случайной величине
содержится в дискретной случайной величине  , где независимые дискретные случайные величины
, где независимые дискретные случайные величины  и
и  могут с равной вероятностью принимать значение либо 0, либо 1? Найти
могут с равной вероятностью принимать значение либо 0, либо 1? Найти  и
и 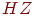 . Каков характер зависимости между
. Каков характер зависимости между  и
и 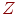 ?
?
Упражнение 8 Дискретные случайные величины  ,
,  - зависимы и распределены также как и соответствующие дискретные случайные величины из предыдущей задачи. Найти
- зависимы и распределены также как и соответствующие дискретные случайные величины из предыдущей задачи. Найти 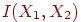 , если совместное распределение вероятностей
, если совместное распределение вероятностей  и
и  описывается законом
описывается законом

Упражнение 9 Дискретные случайные величины  и
и  определяются подбрасыванием двух идеальных тетраэдров, грани которых помечены числами от 1 до 4. дискретная случайная величина
определяются подбрасыванием двух идеальных тетраэдров, грани которых помечены числами от 1 до 4. дискретная случайная величина  равна сумме чисел, выпавших при подбрасывании этих тетраэдров, т.е.
равна сумме чисел, выпавших при подбрасывании этих тетраэдров, т.е.  . Вычислить
. Вычислить  ,
,  и
и  .
.
Упражнение 10 Подсчитать сколько информации об  содержится в дискретной случайной величине
содержится в дискретной случайной величине  , а также
, а также 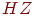 . Дискретные случайные величины
. Дискретные случайные величины  и
и  берутся из предыдущего упражнения.
берутся из предыдущего упражнения.
Упражнение 11 Дискретная случайная величина  может принимать три значения
может принимать три значения 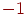 , 0 и 1 с равными вероятностями. Дискретная случайная величина
, 0 и 1 с равными вероятностями. Дискретная случайная величина  с равными вероятностями может принимать значения 0, 1 и 2.
с равными вероятностями может принимать значения 0, 1 и 2.  и
и  - независимы.
- независимы.  . Найти
. Найти  ,
,  ,
,  ,
,  ,
,  .
.
Упражнение 12Найти энтропии дискретных случайных величин 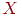 ,
,  ,
, 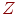 и количество информации, содержащейся в
и количество информации, содержащейся в  относительно
относительно  .
. 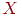 и
и  - независимы и задаются распределениями
- независимы и задаются распределениями
