 |
|
Потрібно було довести.
Приклад. Дослідити збіжність числового ряду
 .
.
Розв’язування. Загальний член ряду  Знайдемо при
Знайдемо при  його границю :
його границю :

Отже, даний ряд є розбіжним.
Відмітимо, що 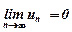 є лише необхідною умовою збіжності числового ряду, але не достатньою. Це означає, що дана умова може виконуватися, але відповідний числовий ряд може бути розбіжним.
є лише необхідною умовою збіжності числового ряду, але не достатньою. Це означає, що дана умова може виконуватися, але відповідний числовий ряд може бути розбіжним.
Прикладом єгармонічний ряд  .
.
Як бачимо, необхідна умова для цього ряду виконується:
 , однак він є розбіжним .
, однак він є розбіжним .
Існує декілька ознак, які дозволяють стверджувати збіжність або розбіжність числових рядів.
Достатні ознаки збіжності числових рядів
З додатними членами
Ознака порівняння рядів
ТЕОРЕМА. Якщо кожний член ряду
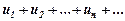 (8.10)
(8.10)
З додатними членами менший (або рівний) відповідного члена
Збіжного ряду
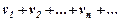 (8.11)
(8.11)
З додатними членами, то ряд (8.10) збігається.
Якщо кожний член ряду (8.10) більший (або рівний) відповідного члена розбіжного ряду (8.11), то ряд (8.10) розбігається.
Доведення. Нехай  і ряд (8.11) збігається. Складемо суми перших
і ряд (8.11) збігається. Складемо суми перших 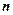 членів рядів (8.10) і (8.11):
членів рядів (8.10) і (8.11):


Оскільки  то
то 
Ряд (8.11) збігається, то  Звідси випливає, що
Звідси випливає, що  При необмеженому зростанні номера
При необмеженому зростанні номера 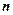 послідовність сум
послідовність сум  як зростаюча послідовність і обмежена звер- ху числом
як зростаюча послідовність і обмежена звер- ху числом 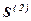 , має границю
, має границю  тобто
тобто  а тому ряд (8.10) також збігається.
а тому ряд (8.10) також збігається.
Нехай  і ряд (8.11) розбігається. Тоді в силу нерівностей
і ряд (8.11) розбігається. Тоді в силу нерівностей  випливає, що
випливає, що  Але оскільки
Але оскільки 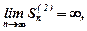 то
то  також буде необмежено зростати , тобто ряд буде розбігатися.
також буде необмежено зростати , тобто ряд буде розбігатися.
Приклад 1. Дослідити збіжність ряду


Розв’язування. Порівняємо даний ряд з нескінченно спадною геометричною прогресією

Оскільки  для довільного
для довільного 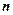 , а ряд нескінченно спадної геометричної прогресії є збіжним рядом, то згідно з ознакою порівняння рядів вихідний ряд буде збіжним.
, а ряд нескінченно спадної геометричної прогресії є збіжним рядом, то згідно з ознакою порівняння рядів вихідний ряд буде збіжним.
Приклад 2.Дослідити збіжність ряду
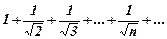
Розв’язування. Даний ряд порівняємо з гармонічним рядом. Для довільного 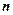 виконується нерівність
виконується нерівність 
Як було показано вище, гармонічний ряд розбігається, отже даний ряд розбігається також.
Ознака Даламбера
ТЕОРЕМА. Нехай всі члени ряду  додатні і нехай при необмеженому зростанні номера
додатні і нехай при необмеженому зростанні номера 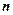 границя відношення
границя відношення  го члена до
го члена до 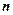 -го існує і дорівнює деякому числу
-го існує і дорівнює деякому числу  , тобто
, тобто  .
.
Тоді :
1. Якщо 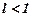 , то ряд збіжний.
, то ряд збіжний.
2. Якщо  , то ряд розбіжний.
, то ряд розбіжний.
3. Якщо 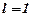 , то ознака не дає відповіді на питання про збіжність або розбіжність ряду, тобто ряд в даному випадку може як збігатися , так і розбігатися.
, то ознака не дає відповіді на питання про збіжність або розбіжність ряду, тобто ряд в даному випадку може як збігатися , так і розбігатися.
Доведення. Нехай маємо ряд
 (8.12)
(8.12)
складений із додатних чисел, і нехай
 . (8.13)
. (8.13)
Тоді при достатньо великому n, тобто при n не меншому деякого числа N маємо:
 , де
, де  - як завгодно мале додатне число. Звідси
- як завгодно мале додатне число. Звідси
 як тільки
як тільки  .
.
а) Нехай l<1. Ми зможемо вибрати число ε  настільки малим, що l+ε також буде менше одиниці, тоді, поклавши l+ε=q, одержимо:
настільки малим, що l+ε також буде менше одиниці, тоді, поклавши l+ε=q, одержимо:
 ,
, 


 і т.д.
і т.д.
Отже,  .
.
Звідси випливає, що члени ряду 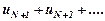 ., які представляють N- ий залишок ряду (8.12), менші відповідних членів нескінченно спадної геометричної прогресії
., які представляють N- ий залишок ряду (8.12), менші відповідних членів нескінченно спадної геометричної прогресії
 (знаменник
(знаменник  .
.
Цей ряд збіжний, отже ряд (8.12) збіжний.
б) Нехай  . Тоді можна підібрати
. Тоді можна підібрати  таким, що при
таким, що при  буде справедлива нерівність
буде справедлива нерівність
 . (8.14)
. (8.14)
де  вибирається настільки малим, щоб величина
вибирається настільки малим, щоб величина  залишалась більшою 1. Тоді кожний наступний член ряду буде більшим за попередній, а це суперечить необхідній ознаці збіжності ряду.
залишалась більшою 1. Тоді кожний наступний член ряду буде більшим за попередній, а це суперечить необхідній ознаці збіжності ряду.
Отже, ряд розбігається.
в) В тому випадку, коли границя l=1, ознака Даламбера не дає відповіді на питання про збіжність чи розбіжність ряду. Ряди можуть бути як збіжними так і розбіжними.
Приклад 1. Дослідити збіжність ряду
 .
.
Розв’язування. Оскільки  , то
, то  , а значить,
, а значить,

Тут 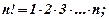


Оскільки  , то згідно з ознакою Даламбера даний ряд збігається.
, то згідно з ознакою Даламбера даний ряд збігається.
Приклад 2. Дослідити збіжність ряду
 .
.
Розв’язування. Тут  ,
,  .
.
Тому


Оскільки l=∞, то за ознакою Даламбера числовий ряд розбігається.
Приклад 3. Дослідити збіжність ряду

Розв’язування. Знаходимо
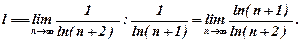
Одержану невизначеність типу  розкриємо за правилом Лопіталя:
розкриємо за правилом Лопіталя:


Тому за ознакою Даламбера збіжність вихідного ряду встановити неможливо. Якщо ознака Даламбера не дає відповіді на питання про збіжність ряду (при l=1), потрібно використати інші ознаки дослідження збіжності даного ряду.