 |
|
Системы линейных уравнений
Линейные образы.
3.1.1. Прямая на плоскости.
3.1.2. Плоскость в пространстве.
3.1.3. Прямая в пространстве.
Кривые второго порядка.
3.2.1. Окружность.
3.2.2. Эллипс.
3.2.3. Гипербола.
3.2.4. Парабола.
Поверхности второго порядка.
Преобразование координат.
3.4.1. Преобразование координат на плоскости.
3.4.2. Преобразование координат в пространстве.
4. Комплексные числа……………………………………………………………………..20
4.1. Алгебраическая форма комплексного числа.
4.2. Действия над комплексными числами в алгебраической форме.
4.3. Тригонометрическая форма комплексного числа.
4.4. Показательная форма комплексного числа.
4.5. Действия над комплексными числами в тригонометрической и показательной форме.
5. Введение в анализ………………………………………………………………………22
5.1. Функции. Общие свойства.
5.2. Основные элементарные функции.
5.3. Теория пределов.
5.4. Непрерывность функции.
6. Дифференциальное исчисление…………………………………………………..28
6.1. Определение производной.
6.2. Основные правила дифференцирования.
6.3. Производные основных элементарных функций.
6.4. Гиперболические функции.
6.5. Производные высших порядков и формула Тейлора.
6.6. Исследование функций.
7. Интегральное исчисление……………………………………………………………34
Неопределённый интеграл.
7.1.1. Определения и свойства.
7.1.2. Основные методы интегрирования.
7.1.3. Таблица интегралов.
Определённый интеграл.
7.2.1. Определения и свойства.
7.2.2. Приложения определённого интеграла.
| Тема 1. Линейная алгебра |
Определители (детерминанты)
Обозначения определителя матрицы А: D , det A,  .
.
Определитель второго порядка:  .
.
Определитель третьего порядка:


Разложение определителя n-го порядка по i-й строке: 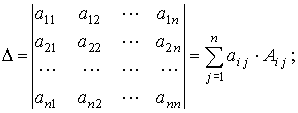
Разложение определителя n-го порядка по j-ому столбцу:
 -алгебраическое дополнение элемента
-алгебраическое дополнение элемента  ,
,  ,
,
 -минор элемента
-минор элемента  , т.е. определитель, получаемый из исходного определителя вычёркиванием i-й строки и j-го столбца.
, т.е. определитель, получаемый из исходного определителя вычёркиванием i-й строки и j-го столбца.
Матрицы
Равенство матриц:  , если эти матрицы одного размера и
, если эти матрицы одного размера и  .
.
Квадратная матрица порядка n:  .
.
Сложение матриц:  , где
, где  .
.
Свойства сложения матриц:
1) ассоциативность:  ;
;
2) коммутативность:  ;
;
Умножение матрицы на число:  .
.
Умножение матриц:  .
.
Свойства умножения матриц:
- ассоциативность:
 ;
; - некоммутативность.
- определитель произведения квадратных матриц:
 .
.
Транспонирование матрицы:  .
.
Свойство транспонирования произведения матриц: 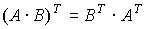 .
.
Невырожденная (неособая) матрица:  .
.
Обратная матрица для невырожденной матрицы A: 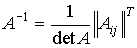 .
.
Свойства обратной матрицы:
1)  ;
;
2)  .
.
Виды матриц:
единичная матрица: 
симметрическая матрица: 

ортогональная матрица: A - невырождена и 
кососимметрическая матрица:  ;
;
матрица-строка: 
матрица-столбец:  .
.
Ранг матрицы  - наибольший порядок её ненулевого минора или наибольшее число линейно независимых строк (столбцов) матрицы.
- наибольший порядок её ненулевого минора или наибольшее число линейно независимых строк (столбцов) матрицы.
Системы линейных уравнений

| 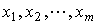 - неизвестные;
aij –коэффициент в i-ом уравнении при j-ом неизвестном; - неизвестные;
aij –коэффициент в i-ом уравнении при j-ом неизвестном;
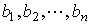 - свободные члены. - свободные члены.
|
Матричный вид:  ,
, 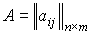 - матрица системы,
- матрица системы,

| - столбец неизвестных, | 
| - столбец свободных членов. |
Совместность системы:  , где
, где 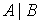 - расширенная матрица системы (теорема Кронекера-Капелли).
- расширенная матрица системы (теорема Кронекера-Капелли).
Формулы Крамера (n=m):  ,
,
 - определитель матрицы системы;
- определитель матрицы системы;
 -определитель, полученный при замене i-го столбца матрица A на столбец В.
-определитель, полученный при замене i-го столбца матрица A на столбец В.
Однородная система (B=0):

| Если  , то система им , то система им  еет только нулевое решение .
Если еет только нулевое решение .
Если  , то существуют ненулевые решения. , то существуют ненулевые решения.
|
| Тема 2. Векторная алгебра |
| Наименование | Обозначение, формула |
| Вектор и его выражение в декартовых координатах | a=ax i+ay j+az k=(ax, ay, az) |
| Модуль (длина) вектора | 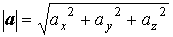
|
| Направляющие косинусы вектора | 
|
| Сложение двух векторов | a+b=(ax+bx, ay+by ,az+bz) |
| Умножение вектора на скаляр | ka=(kax, kay, kaz) |
| Скалярное произведение двух векторов | 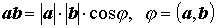
|
| Скалярное произведение в декартовых координатах | ab=axbx+ayby+azbz |
| Условие ортогональности двух ненулевых векторов | ab=0  a a  b b
|
| Векторное произведение двух векторов | 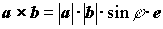
 , e , e  a, e a, e  b e - единичный вектор a, b, e - правая тройка векторов b e - единичный вектор a, b, e - правая тройка векторов
|
| Векторное произведение в декартовых координатах | 
|
| Условие коллинеарности двух ненулевых векторов |  a| | b a| | b
|
| Смешанное произведение трех векторов | 
|
| Смешанное произведение в декартовых координатах | 
|
| Условие компланарности трех ненулевых векторов | abc=0  a, b, c - компланарныe векторы (лежат в одной плоскости) a, b, c - компланарныe векторы (лежат в одной плоскости)
|
| Линейно независимая система векторов | {a1,a2,…,an} - линейно независима  только при условии только при условии  . .
|
| Тема 3. Аналитическая геометрия |
Линейные образы
3.1.1. Прямая на плоскости
Виды уравнений
| Уравнение | Наименование | Параметры |

| общее уравнение прямой на плоскости | n=(A,B) - нормальный вектор прямой;
 , ,  , ,  - координаты фиксированных точек на прямой;
k - угловой коэффициент прямой;
a - отрезок, отсекаемый прямой на оси х;
b - отрезок, отсекаемый прямой на оси y;
q=(l,m) - направляющий вектор прямой - координаты фиксированных точек на прямой;
k - угловой коэффициент прямой;
a - отрезок, отсекаемый прямой на оси х;
b - отрезок, отсекаемый прямой на оси y;
q=(l,m) - направляющий вектор прямой
|

| уравнение прямой, проходящей через данную точку | |

| уравнение прямой с данным угловым коэффициентом | |

| уравнение прямой, проходящей через данную точку с данным угловым коэффициентом | |
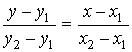
| уравнение прямой, проходящей через две точки | |

| уравнение прямой в отрезках | |

| каноническое уравнение прямой |
Формулы для вычисления угла между двумя прямыми на плоскости:
 ;
;  ,
,
где  и
и  -нормальный и направляющий векторы первой прямой;
-нормальный и направляющий векторы первой прямой;
 и
и  - нормальный и направляющий векторы второй прямой.
- нормальный и направляющий векторы второй прямой.
Условия параллельности двух прямых на плоскости:
-
 ;
; -
 ;
; -
 , где
, где  и
и 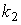 - угловые коэффициенты прямых.
- угловые коэффициенты прямых.
Условия перпендикулярности двух прямых на плоскости:
- n1
 n2
n2  n1
n1 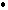 n2=0 или A1A2+B1B2=0;
n2=0 или A1A2+B1B2=0; - q1
 q2
q2  q1
q1 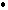 q2=0 или l1l2+m1m2=0;
q2=0 или l1l2+m1m2=0; -

3.1.2. Плоскость в пространстве
Виды уравнений
| Уравнение | Наименование | Параметры |

| общее уравнение плоскости в пространстве |  - нормальный вектор плоскости; - нормальный вектор плоскости;
  - координаты фиксированных точек на плоскости;
a,b,c – отрезки, отсекаемые плоскостью на осях координат; - координаты фиксированных точек на плоскости;
a,b,c – отрезки, отсекаемые плоскостью на осях координат;
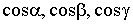 - направляющие косинусы нормального вектора плоскости;
p - длина перпендикуляра, опущенного из начала координат на плоскость - направляющие косинусы нормального вектора плоскости;
p - длина перпендикуляра, опущенного из начала координат на плоскость
|
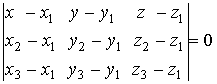
| уравнение плоскости, проходящей через три точки | |
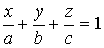
| уравнение плоскости в отрезках | |


| нормальное уравнение плоскости |
Выражение направляющих косинусов через координаты нормального вектора:

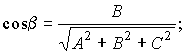
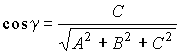 .
.
Формулы для вычисления угла между двумя плоскостями:
 ;
;
где  и
и  -нормальные векторы плоскостей.
-нормальные векторы плоскостей.
Условие параллельности двух плоскостей:
 .
.
Условие перпендикулярности двух плоскостей:
n1  n2
n2  n1
n1 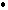 n2=0 или A1A2+B1B2+С1С2=0.
n2=0 или A1A2+B1B2+С1С2=0.
3.1.3. Прямая в пространстве
Виды уравнений
| Уравнение | Наименование | Параметры |

| общие уравнения прямой в пространстве | 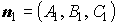 и и 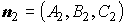 - нормальные векторы плоскостей; - нормальные векторы плоскостей;
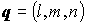 - направляющий вектор прямой; - направляющий вектор прямой;
 , ,  , ,  - координаты фиксированных точек на прямой - координаты фиксированных точек на прямой
|

| канонические уравнения прямой в пространстве | |

| параметрические уравнения прямой в пространстве | |

| уравнения прямой, проходящей через две фиксированные точки |
Формулы для вычисления угла между двумя прямыми в пространстве:
 ,
,
где  и
и  - направляющие векторы прямых.
- направляющие векторы прямых.
Условие параллельности двух прямых в пространстве:
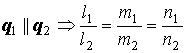 .
.
Условие ортогональности двух прямых в пространстве:
q1  q2
q2  q1
q1  q2=0 или l1l2+m1m2+n1n2=0.
q2=0 или l1l2+m1m2+n1n2=0.
| Тема 3. Аналитическая геометрия |