Главная | Обратная связь

ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ

Ø Уравнение гармонических колебаний:

где х – смещение колеблющейся величины от положения равно­весия; А – амплитуда колебаний

Ø Гармонические колебанияв графическом виде:

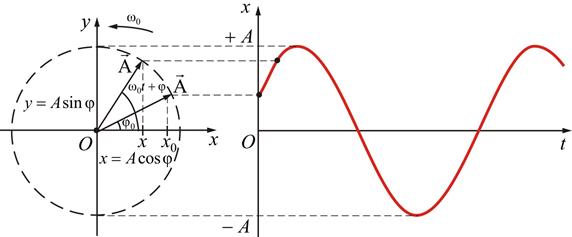
Ø Частота колебаний – число последовательных колебаний в одну секунду:

.

Ø Циклическая (круговая) частота колебаний – число полных колебаний за 2π секунд:

.

Ø Период колебаний – минимальный промежуток времени, по истечению которого повторяются значения всех физических величин, характеризующих колебания:

.

Ø Скорость колебаний:

.

Ø Ускорение колебаний:

.

Ø Амплитуда скорости:

.

Ø Амплитуда ускорения:

.

Ø Уравнение движения материальной точки:

.

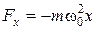Ø Квазиупругая сила:

.

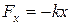Ø Дифференциальное уравнениединамики гармонических колебаний материальной точки под действием упругих и квазиупругих сил:

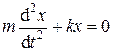или .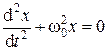

Ø Циклическая частота незатухающих колебаний:

.

Ø Период незатухающих колебаний:

.

Ø Потенциальная энергияЕ_птела:

.

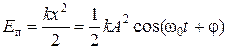Ø Кинетическая энергия тела:

.

Ø Полная механическая энергия материальной точки, совершающей гармонические колебания:

.

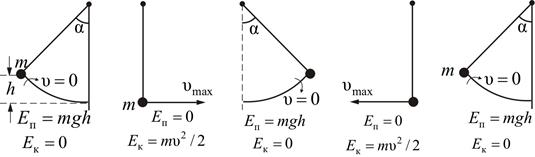
Ø Математический маятник – идеализированная система, состоящая из невесомой нерастяжимой нити, на которую подвешена масса, сосредоточенная в одной точке (шарик на длинной тонкой нити).

Ø Уравнение динамики вращательного движения математического маятника:

.

Ø Вращающий момент стремится вернуть маятник в положение равновесия, он возникает при отклонении тела от положения равновесия на угол α:

,

где l – расстояние между точкой подвеса и центром масс маятника С.

Ø Момент инерции маятника:

.

Ø Угловое ускорение:

.

Ø Дифференциальное уравнение математического маятника:

;

· решение данного уравнения:

.

Ø Циклическая частота математического маятника:

.

Ø Период колебаний математического маятника:

· в инерциальной системе отсчета:

;

· в неинерциальной системе отсчета:

Ø Циклическая частота физического маятника физический маятник – (это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси, проходящей через точку О, не совпадающие с центром масс С):

.

Ø Период колебаний физического маятника:

.

Ø Приведенная длина физического маятника:

.