Главная | Обратная связь

Круги Мора для деформированного состояния

Графическое предстовление о совокупности G и τ даёт диаграмма Морра

G_н – по оси абсцисс (х)

τ- по оси ординат (y)

G_н = S_x*a_x+S_y*a_y+S_z*a_z

G_x*a_x²+τ_xy*a_y*a_x+τ_xz*a_z*a_x+τ_yx*a_x*a_y+G_y*a_y²+τ_yz*a_z*a_y+τ_zx*a_x*a_z+τ_zy*a_y*a_z+Gz_az²

2τ_zy*a_y*a_z+2τ_yx*a_x*a_y+2τ_xz*a_z*a_x+G_x*a_x² +G_y*a_y²+G_z*a_z²

Параметрические уравнения наибольшего из кругов Мора имеют вид:

Из этого следует уравнение окружности Мора для деформации:

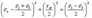
На рис. 3.31 дано геометрическое изображение кругов деформаций Мора, из которых следует:

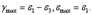(92)

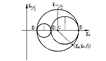
Рис. 3.31

 

Величина:

называется параметром Лоде для деформированного состояния. Она характеризует вид деформированного состояния.

Радиусы кругов Мора дают экстремальные значения сдвигов

Тензор деформаций. Его составляющие.

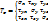
Тензор напряжений-это функция определяющая напряжение для любой площадки, проходящей через данную точку

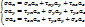
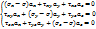
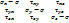=0

Тензор напряжений имеет 3 инварианта. 1-линейный 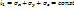2-квадратичный 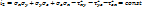3-кубический 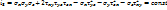3-кубический

 

14) Понятие об инвариантах тензора деформаций.

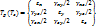
Деформированное Состояние в точке = тензору деформации с компонентами линейные и угловые деформации.

-тензор при главных напряжениях

Шаровой тензор деф-ции(изменение объема)

Девиатор: изменение формы)

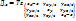
3инварианта: линейный,квадратичный и кубический.

Линейный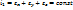
Квадратичный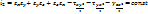
кубический: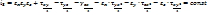
Схема главных деформаций

Существует 3 вида схем главных деф-ций.
1) схемы у которых 1 главная деф-ция положительная, а 2 другие отриц.(растяжение).
2) одна главная деф-ция равна 0,а две др. равны по абсолютной велечине но разные по знаку.(плоское сост.-сдвиг)
3)1отриц а 2ост. Положительные(сжатие)

1и 3 виды-объемные схемы.

Простое растяжение- 2 отриц. Деф-ции равны.

Простое сжатие – 2 положит. Деф-ции равны.

-1 вид < <1 – 3 вид