 |
|
МАТЕМАТИЧЕСКАЯ ОБРАБОТКА ДАННЫХ ЭКСПЕРИМЕНТОВ
Метод оптимального планирования
Этот статистический метод включает следующие этапы исследования [3].
Создается математическая модель, описывающая поведение системы. Модель может не иметь силы закона как некоторой абсолютной истины, присущей точным наукам; она может давать лишь какое-то представление о поведении неорганизованной системы с изменением ряда факторов и составляется на основе имеющихся исследований.
Математическая модель не описывает систему в целом, а лишь определенный комплекс факторов, наиболее интересующих исследователя, стремящегося создать по возможности более простую модель.
Так изменение стойкости инструмента Т в зависимости от скорости резания V, подачи S и глубины резания t описывается математической моделью:
, (6.1)
где Т – зависимая и V, S, t – независимые переменные.
В логарифмическом масштабе уравнение будет полиномом первой степени
(6.2)
Или, учитывая ошибки эксперимента 
,
. (6.3)
Эксперименты планируются на основе многофакторного анализа, т.е. одновременного варьирования всех переменных факторов 
, 
, 
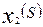. Необходимо определить постоянную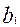 
, 
, 
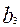. Каждая из трех переменных варьируется на двух или трех уровнях ( 
и 
), где к – число переменных. Принимается вариант первый.
План двенадцати опытов, предусматривающий две серии по шесть опытов в каждой – четыре основных и два дополнительных.
Выбор режимов резания производится таким образом, чтобы упростить кодирование с учетом возможностей станка и предельных режимов резания, как это показано в таблице 6.1.
Режимы резания и кодовые обозначения
Таблица 6.1
| Уровень | Режимы резания | Кодовые обозначения | ||||
| V | S | T | X1 | X2 | X3 | |
| м/мин | мм/об | мм | ||||
| Верхний | 0,50 | 2,50 | ||||
| Средний | 0,37 | 1,75 | ||||
| Нижний | 0,25 | 1,25 | -1 | -1 | -1 |
Эти уровни закодированы при помощи уравнений преобразования таким образом, чтобы верхний уровень соответствовал +1, а нижний –1;
 |
(6.4)
.
Здесь в плане эксперимента, например, за единицу скорости резания принята величина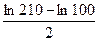 
. Таким образом, скорость резания V преобразуется путем деления ее на принятую единицу. Аналогично поступают с подачей S и глубиной резания t.
Для упрощения расчетов композиционный план строится согласно так называемому «итальянскому кубу», построенному на трех ортогональных координатах с началом координат в центре куба (рис. 6.1).
Рис. 6.1. Композиционный план исследований согласно «итальянскому кубу» (на вершинах куба обозначены номера опытов и режимов резания (1-12))
Опытные точки задаются вершинами правильного симплекса. На рисунке 6.1. они обозначены зачерненными кружками, согласно первым четырем опытам. Далее если результаты двух дополнительных опытов, проставленные в центре куба для проверки гипотезы адекватности не соответствуют требования, выполняется еще шесть опытов: достраиваются вершины куба (обозначены кружками) и еще два опыта в центре.
Условия резания, обозначения и стойкость резцов
Таблица 6.2
| № опыта | № серии | Режимы резания | Кодовые обозначения | Т | y=lnT | |||||
| V | S | t | X1 | X2 | X3 | |||||
| м/мин | мм/об | мм | мин | |||||||
| 0,25 | 1,25 | -1 | -1 | -1 | 5,08 | |||||
| 0,25 | 1,25 | -1 | -1 | 3,61 | ||||||
| 0,50 | 1,25 | -1 | -1 | 5,11 | ||||||
| 0,50 | 1,25 | -1 | 3,30 | |||||||
| 0,25 | 2,5 | -1 | -1 | 5,15 | ||||||
| 0,25 | 2,5 | -1 | 3,56 | |||||||
| 0,50 | 2,5 | -1 | 4,79 | |||||||
| 0,50 | 2,5 | 2,89 | ||||||||
| 0,37 | 1,75 | 4,19 | ||||||||
| 0,37 | 1,75 | 4,42 | ||||||||
| 0,37 | 1,75 | 4,26 | ||||||||
| 0,37 | 1,75 | 4,41 |
В табл.6.2 приводятся результаты 12 опытов по резанию углеродистой стали твердосплавным резцом. За критерий затупления резца принята фаска износа по задней поверхности резца 
мм.
Оценка параметров
На основании результатов серии №1 из шести опытов удобно оценить четыре коэффициента в постулированной эмпирической формуле.
, (6.5)
пользуясь методом наименьших квадратов и свойствами скалярного произведения основных векторов.
Матрица независимых переменных x для серии №1 из шести опытов имеет вид.
Таблица 6.3
| X0 | X1 | X2 | X3 | №опыта | Т | y=lnT | |
| мин | |||||||
| X= | -1 | -1 | 3,61 | ||||
| -1 | -1 | 5,11 | |||||
| -1 | -1 | 5,15 | |||||
| 2,89 | |||||||
| 4,19 | |||||||
| 4,42 |
Согласно методу наименьших квадратов необходимо, чтобы сумма квадратов отклонений фактических значений y от формальных, полученных по уравнению (6.3) 
была наименьшей, т.е.
. (6.6)
Левую часть выражения (7.6) обозначим буквой f (f-функция от неизвестных параметров 
, , , ).
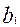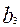Минимум этой функции найдем из уравнений
; 
; 
; 
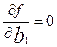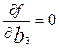. (6.7)
Продифференцировав, напишем систему этих уравнений в окончательном виде:
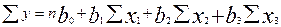
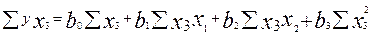
Уравнения (7.8) дают возможность определить 
где – n число опытов; в нашем примере n=6.
; 
; 
(6.9)
Необходимо добавить, что другие члены уравнений будут равны нулю в силу ортогональности векторов 
, 
, 
и 
Очевидно: было бы проще не решать уравнения (6.6) (6.8), а воспользоваться матрицами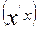 
и 
.
Согласно уравнениям (6.9), имеем:
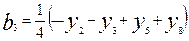
Здесь индексы при y обозначают номера опытов (таблица 6.2)
Подставив в последние уравнения опытные значения из серии №1, можно получить формулу для стойкости резца:
(6.10)
Формулу (6.10) необходимо расшифровать, согласно уравнениям (6.4):
Подставляя значения , , в уравнение (6.10), получим
Следовательно
мин (6.11)
После статистического анализа результатов серии №1 опытов, когда выявились слишком большие интервалы колебаний стойкости при 95% достоверности, были выполнены еще шесть опытов серии №2 исследований. В результате всех опытов получена формула:
мин , (6.12)
Формула мало отличается от формулы (6.11), но 95%-ные доверительные интервалы значительно улучшились, благодаря большему числу опытов.