Главная | Обратная связь

Определение функционального ряда. Область сходимости. Равномерная сходимость

Г л а в а 2. Функциональные ряды

 

 

Определение 1.

Пусть дана последовательность функций 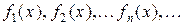. Выражение в виде бесконечной суммы

или (*)

называется функциональным рядом.

При любом значении из области определения членов ряда получается числовой ряд, сходимость которого можно исследовать. Напомним, что ряд может сходится как условно, так и абсолютно.

Определение 2.

Множество значений , для которых ряд (*) сходится, называется областью сходимости ряда.

Обозначим область сходимости ряда (*) . Каждому отвечает значение суммы ряда (*), тем самым на множестве определена функция ─ сумма функционального ряда. Обозначим частичные суммы ряда (*) , а остаток ряда . Если ряд сходится, то .

Примеры.

1) . .

Очевидно, что область сходимости, причем абсолютной, .

2). ─ сходится условно при всех .

Определение 3.

Ряд (*) называется равномерно сходящимся на множестве , если для такой номер , такой, что при всех и всех выполняется неравенство .

Иначе, остаток ряда оказывается сколь угодно мал сразу для всех , если достаточно велико.

Для примера исследуем на равномерную сходимость ряд .

Найдем остаток .

Ясно, что при . Теперь при фиксированном найдем пределы

, .

Значения этих пределов говорят о том, что остаток ряда не может быть сколь угодно малым сразу для всех , какой бы большой номер ни взять. Значит, ряд сходится неравномерно.

Запомним:

1). Ряд сходится абсолютно при , но неравномерно.

 

2). Остаток сходящегося знакочередующегося ряда не превышает по модулю первого отброшенного члена, поэтому . Очевидно, что модуль остатка может стать сколь угодно малым при достаточно большом . Итак, этот ряд сходится равномерно, но условно.

Равномерная сходимость играет важную роль в исследовании функции ─ суммы функционального ряда. Приведем признак равномерной сходимости.

 

Теорема. (Признак Вейерштрасса равномерной сходимости)

Если для каждого члена ряда (*) существует число такое, что , причем числовой ряд сходится, то ряд (*) сходится равномерно и абсолютно.

Доказательство.

Неравенство означает, что ряд является мажорантой ряда , значит, ряд (*) сходится абсолютно.

Покажем теперь, что остаток функционального ряда (*) оценивается через остаток числового ряда . Для некоторого запишем

.

 

При получим , где ─ остаток ряда . По условию теоремы ряд сходится, поэтому для такой номер , такой, что при всех выполняется неравенство , а, значит и сразу для всех . ■

 

Замечание. Признак Вейерштрасса равномерной сходимости не является необходимым, что показывает пример ряда , который сходится равномерно, но условно, т.е. не обладает сходящейся мажорантой.

Рассмотрим ряд при где любое фиксированное число.

При верно неравенство . Числовой ряд сходится, поэтому ряд сходится равномерно при для любого , .