 |
|
Г л а в а 3. Степенные ряды
§1. Определение степенного ряда. Область сходимости и радиус сходимости. Равномерная сходимость
Функциональный ряд вида 
называется степенным. Число 
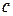называется центром ряда, а числа 
─ коэффициентами ряда. Замена переменной 
приводит ряд к виду 
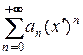, т.е к ряду с нулевым центром. Далее будем рассматривать именно такие ряды.
Итак, пусть дан ряд
. (*)
Выясним, какую область сходимости он имеет и каковы функциональные свойства суммы ряда. Заметим сразу, что область сходимости не является пустым множеством ─ при 
ряд (*) всегда сходится.
Теорема 1.(Первая теорема Абеля)
Если ряд (*) сходится в точке 
, то он сходится при всех 
, причем абсолютно.
Доказательство.
Числовой ряд 
сходится 
выполнен необходимый признак, т.е. 
величина 
ограничена существует 
такое, что 
.
Запишем цепочку неравенств
. При всех 
, таких, что 
, ряд 
сходится ( сумма бесконечно убывающей геометрической прогрессии), поэтому сходится ряд 
для всех 
, что и означает, что сходится абсолютно ряд (*), т.е. он сходится. ■
Следствие.Если ряд (*) расходится в точке , то он расходится при всех 
.
Доказать самостоятельно.
Пусть 
─ область сходимости ряда (*). Найдем 
. Очевидно, что 
. Рассмотрим возможные случаи.
При 
ряд (*) сходится только при . Примером является ряд 
.
При 
ряд сходится при любых . Примером является ряд 
.
Пусть теперь 
. Возьмем 
. По определению точной верхней грани для 
найдется такое 
, что 
, и ряд сходится (точную верхнюю грань нельзя уменьшить!).
По первой теореме Абеля ряд (*) сходится при 
, т.е ряд сходится в интервале 
, и, значит, сходится в точке 
. Поэтому заключаем, что областью сходимости ряда (*) является интервал 
.
Определение .
Величина 
называется радиусом сходимости степенного ряда.
Итак, степенной ряд 
с радиусом сходимости сходится при 
, причем абсолютно, расходится при 
. При 
и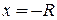 
сходимость зависит от конкретного ряда.
Примеры.
1. 
. Исследуем сходимость по признаку Даламбера:
. Ряд сходится при 
и расходится при 
. Посмотрим граничные точки 
и 
. Нетрудно видеть, что в обоих случаях не выполняется необходимый признак сходимости, т.е. ряд расходится.
Ответ.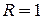 
; область сходимости .
2. 
.
Найдем по признаку Даламбера
. Ряд сходится при 
.
Исследуем сходимость в точке 
. Имеем ряд 
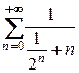. Видно, что этот ряд эквивалентен гармоническому ряду 
, значит, он расходится.
Теперь рассмотрим случай 
. Получаем знакочередующийся ряд 
. Обратимся к признаку Лейбница. Условия 1 и 3 , очевидно, выполнены, проверим условие 2 ─ монотонность стремления к 0. Для этого исследуем функцию 
. Найдем производную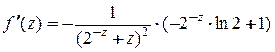 
. Видно, что 
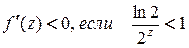, следовательно, эта функция монотонно убывает при 
, и дробь 
также убывает при 
. Итак, условия признака Лейбница выполнены ─ ряд 
сходится (условно!).
Ответ. 
; область сходимости 
.
Теорема 2.(Равномерная сходимость степенного ряда)
Степенной ряд сходится равномерно внутри интервала сходимости, т.е. для 
степенной ряд сходится равномерно на отрезке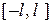 
.
Доказательство.
Так как 
при 
, то числовой положительный сходящийся ряд 
является мажорантой ряда на отрезке 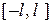, поэтому ряд (*) по признаку Вейерштрасса сходится равномерно.
Теорема 3.(Вторая теорема Абеля)
Если степенной ряд с радиусом сходимости сходится, пусть и условно при ( 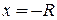), то он сходится равномерно вплоть до этой точки, т.е. равномерно сходится, например, на отрезке 
.
(Без доказательства)
§2.Свойства суммы степенного ряда
Пусть степенной ряд имеет радиус сходимости .
Мы уже знаем, что степенной ряд сходится равномерно на любом отрезке внутри интервала сходимости, поэтому из теорем о непрерывности и интегрируемости суммы функционального ряда сразу следует:
1. Сумма 
непрерывна при 
.
2. Степенной ряд можно интегрировать почленно по любому отрезку 
, т.е. 
Теперь обратимся к дифференцированию степенного ряда. Для этого требуется равномерная сходимость ряда из производных, т.е. ряда 
.
Выпишем для наглядности три ряда
(А) 
, радиус сходимости ;
(А1) 
, радиус сходимости обозначим 
;
(А2) 
, радиус сходимости обозначим 
.
Исследуем сходимость ряда (А 1). Зафиксируем 
и возьмем такое 
, что 
. Найдем
, где 
ограничивает общий член сходящегося ряда 
. Легко показать, что ряд 
сходится по признаку Даламбера, если 
. Следовательно, ряд из производных (А1) сходится для и его радиус сходимости не меньше ,т.е. 
.
Теперь сравним ряд (А) с рядом (А2), который получается из (А) умножением на 
:
. Но т.к. 
, то 
. Окончательно, 
.
Таким образом, имеем