Главная | Обратная связь

ОСНОВНЫЕ ТЕОРЕМЫ О ЧИСЛОВЫХ РЯДАХ

ЧИСЛОВЫЕ РЯДЫ

 

 

Методические указания к практическим занятиям

по дисциплине «Высшая математика»

 

Составители: Егорова Ю.Б.

Мамонов И.М.

Корниенко Л.И.

 

МОСКВА 2005

 

 

ВВЕДЕНИЕ

 

Методические указания предназначены для студентов дневного и вечернего отделения факультета № 14 специальностей 071000, 130200, 220200.

 

 

ОСНОВНЫЕ ПОНЯТИЯ

 

Пусть u₁, u₂, u₃, …, u_n, … - бесконечная числовая последовательность. Выражение называется бесконечным числовым рядом, числа u₁, u₂, u₃, …, u_n - членами ряда; называется общим членом ряда. Ряд часто записывают в сокращенном (свернутом) виде: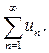

Сумму первых n членов числового ряда обозначают через и называют n-й частичной суммой ряда:

.

Ряд называется сходящимся, если его n-я частичная сумма при неограниченном возрастании n стремится к бесконечному пределу, т.е. если 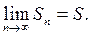Число называют суммой ряда.

Если же n-я частичная сумма ряда при не стремится к конечному пределу, то ряд называют расходящимся.

 

Пример 1.Найти сумму ряда .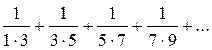

Решение. Имеем . Так как:

,

то

.

Следовательно,

Так как , то ряд сходится и его сумма равна .

 

ОСНОВНЫЕ ТЕОРЕМЫ О ЧИСЛОВЫХ РЯДАХ

 

Теорема 1. Если сходится ряд то сходится и ряд получаемый из данного ряда отбрасыванием первых членов (этот последний ряд называют -м остатком исходного ряда). И наоборот, из сходимости -го остатка ряда вытекает сходимость данного ряда.

Теорема 2. Если сходится ряд 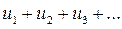и суммой его является число , то сходится и ряд причем сумма последнего ряда равна .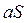

Теорема 3. Если сходятся ряды 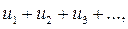имеющие соответственно суммы S и Q, то сходится и ряд причем сумма последнего ряда равна .

Теорема 4 (Необходимый признак сходимости ряда). Если ряд сходится, то , т.е. при предел общего члена сходящегося ряда равен нулю.

Следствие 1. Если 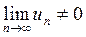, то ряд расходится.

Следствие 2. Если , то определить сходимость или расходимость ряда с помощью необходимого признака сходимости нельзя. Ряд может как сходящимся, так и расходящимся.

 

Пример 2.Исследовать сходимость ряда:

Решение. Находим общий член ряда . Так как:

,

т.е. , то ряд расходится (не выполняется необходимое условие сходимости).