Главная | Обратная связь

Матрицы и операции над ними.

НЕДЕЛЯ 1

Лекция 1.

Определение. Матрицей называется множество чисел, которое составляет прямоугольную таблицу, состоящее из m строк и n столбцов

коротко матрицу обозначают так:

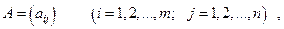
где элементы данной матрицы, i – номер строки, j – номер столбца.

Если в матрице число строк равно числу столбцов (m = n), то матрица называется квадратной n-го порядка, а в противном случае – прямоугольной.

Если m=1 и n >1, то получаем однострочную матрицу

которая называется вектор-строкой, если, же m>1 и n=1, то получаем одностолбцовую матрицу

,

которая называется вектор-столбцом.

Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется диагональной.

Диагональная матрица, у которой элементы главной диагонали равны единице, называется единично, обозначается E.

Матрица, полученная из данной заменой ее строки столбцом с тем же номером, называется транспонированной к данной. Обозначается .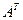

Две матрицы и равны, если равны между собой элементы, стоящие на одинаковых местах, то есть если

при всех i и j (при этом число строк (столбцов) матриц A и B должно быть одинаковым).

1°. Суммой двух матриц A=(a_ij) и B=(b_ij) с одинаковым количеством m строк и n столбцов называется матрица C=(c_ij), элементы которой определяются равенством

Сумму матриц обозначают C=A+B.

Пример.

.

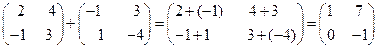2⁰. Произведением матрицы A=(a_ij) на число λ называется матрица, у которой каждый элемент равен произведению соответствующего элемента матрицы A на число λ:

λA=λ(a_ij)=(λa_ij), (i =1,2…,m ; j=1,2…,n ).

Пример.

3⁰. Произведением матрицы A=(a_ij), имеющей m строк и k столбцов, на матрицу B=(b_ij), имеющей k строк и n столбцов, называется матрица C=(c_ij), имеющая m строк и n столбцов, у которой элемент c_ij равен сумме произведений элементов i-ой строки матрицы A и j-го столбца матрицы B, то есть

При этом число столбцов матрицы A должно быть равно числу строк матрицы B. В противном случае произведение не определено. Произведение матриц обозначается A*B=C.

Пример.

Для произведения матриц не выполняется равенство между матрицами A*B и B* A, в общем случае одна из них может быть не определена.

Умножение квадратной матрицы любого порядка на соответствующую единичную матрицу не меняет матрицу.

Пример. Пусть , , тогда согласно правилу умножения матриц имеем

=

и

,

откуда заключаем, что

и

Определители.

Пусть дана квадратная матрица третьего порядка:

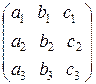(1)

Определение.Определителем третьего порядка, соответствующим матрице (1), называется число, обозначаемое символом

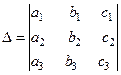
и определяемое равенством

.(2)

Чтобы запомнить, какие произведения в правой части равенства (2) берутся со знаком «+», а какие со знаком «-», полезно использовать следующее правило треугольников.

«+» «-»

 

Пример.

 

Свойства определителей рассмотреть самостоятельно.

 

Определение.Матрица 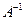называется обратной квадратной матрице A, если .

Определение.Квадратная матрица называется невырожденной, если ее определитель отличен от нуля. В противном случае квадратная матрица называется вырожденной.

Утверждение. Всякая невырожденная матрица имеет обратную.

Элементарными преобразованиями матриц являются:

1. перестановка местами двух параллельных рядов матрицы;

2. умножение всех элементов матрицы на число, отличное от нуля;

3. прибавление ко всем элементами ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число.

 

Матрица В, полученная из матрицы А с помощью элементарных преобразований, называется эквивалентной матрицей.

Элемент строки матрицы называется крайним, если он отличен от нуля, а все элементы строки, находящиеся левее него, равны нулю. Матрица называется ступенчатой, если крайний элемент каждой строки находится правее крайнего элемента предыдущей строки. Например:

- не ступенчатая; - ступенчатая.

 

Ранг матрицы

 

Рассмотрим матрицу Аразмерности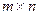

.

Выделим в ней произвольно k строк и k столбцов. Из элементов, стоящих на пересечении выделенных строк и столбцов, составим определитель k-го порядка. Все такие определители называются минорами матрицы А.

Определение.Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы.Обозначается r(A).

Свойства ранга матрицы:

1. При транспонировании матрицы ее ранг не меняется.

2. Если вычеркнуть из матрицы нулевой ряд, то ранг матрицы не изменится.

3. Ранг матрицы не изменится при элементарных преобразованиях матрицы.

4. Ранг ступенчатой матрицы равен количеству ее ненулевых строк.

Литература: К,А, Хасеинов Каноны математики. Стр.5-14, 17-34

 

Лекция 2.