 |
|
Уравнения равновесия
Рассмотрим распространенный частный случай равновесия жидкости, когда на нее действует лишь одна массовая сила, сила тяжести, и получим уравнение, позволяющее находить гидростатическое давление в любой точке рассматриваемого объема жидкости. Если этот объем весьма мал по сравнению с объемом Земли, то свободную поверхность жидкости можно считать горизонтальной плоскостью.
Пусть жидкость содержится в сосуде и на ее свободную поверхность действует давление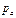 
. Найдем гидростатическое давление 
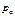в произвольно взятой точке М, расположенной на глубине 
.
Выделим около точки М элементарную горизонтальную площадку dS и построим на ней вертикальный цилиндрический объем высотой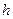 
. Рассмотрим условие равновесия указанного объема жидкости, выделенного из общей массы жидкости. Давление жидкости на нижнее основание цилиндра теперь будет внешним и направлено по нормали внутрь объема, т. е. вверх.
Запишем сумму сил, действующих на рассматриваемый объем в проекции на вертикаль:
.
Последний член уравнения представляет собой вес жидкости в указанном объеме. Силы давления по боковой поверхности цилиндра в уравнение не входят, так как они нормальны к вертикали. Сократив ,выражение на 
,и перегруппировав члены, найдем
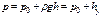(2.2)
Полученное уравнение называют основным уравнением. гидростатики; по нему можно подсчитать давление в любой точке покоящейся жидкости. Это давление, как видно из уравнения, складывается из двух величин: давления 
на внешней поверхности жидкости и давления, обусловленного весом вышележащих слоев жидкости.
Величина является одинаковой для всех точек объема жидкости, поэтому, учитывая свойство гидростатического давления, можно сказать, что давление, приложенное к внешней поверхности жидкости, передается всем точкам этой жидкости и по всем направлениям одинаково. Это положение известно под названием закона Паскаля.
Давление жидкости, как видно из формулы (2.2), возрастает с увеличением глубины по закону прямой и на данной глубине есть величина постоянная.
Поверхность, во всех точках которой давление одинаково, называется поверхностью уровня.В данном случае поверхностями уровня являются горизонтальные плоскости, а свободная поверхность является одной из поверхностей уровня.
Возьмем на произвольной высоте горизонтальную плоскость сравнения, от которой вертикально вверх будем отсчитывать координаты 
. Обозначив через 
координату точки М, через 
координату свободной поверхности жидкости и заменив в уравнении (2.2) h на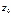 
и 
, получим
. (2.3)
Так как точка М взята произвольно, можно утверждать, что для всего рассматриваемого неподвижного объема жидкости
.
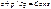Координата 
называетсягеометрической высотой. Величина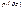 
имеет линейную размерность и называется пьезометрической высотой. Сумма 
) называется гидростатическим напором.
Таким образом, гидростатический напор есть величина постоянная для всего объема неподвижной жидкости.