 |
|
Уравнение Бернулли для установившегося движения жидкости
Основной задачей гидродинамики является изучение законов движения жидкости. Движение жидкости характеризуется скоростями движения частиц и давлением в отдельных точках потока.
Чтобы установить взаимосвязь между основными параметрами движения, а именно между гидродинамическим давлением и скоростью движущейся жидкости, составим уравнения движения жидкости. Эти уравнения могут быть получены из дифференциальных уравнений равновесия жидкости, если к действующим силам согласно принципу д’Аламбера присоединить силы инерции. Получим систему уравнений:
Преобразуем полученные уравнения, применительно к элементарной струйке идеальной жидкости, находящейся в установившемся движении, умножив каждое уравнение соответственно на 
, 
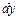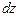. После по членного суммирования получаем
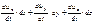
Так как 
, 
, 
- это проекции элементарного пути, проходимого частицами жидкости за время dt, следовательно:
(1.31)
С учетом (3) уравнение (2) примет вид:
(1.32)
- полный дифференциал силовой функции, выражающей массовые силы, под действием которых осуществляется движение жидкости.
- полный дифференциал давления, так как при установившемся движении гидродинамическое давление не зависит от времени.
- полный дифференциал скорости, выраженной через ее составляющие по соответствующим осям координат.
С учетом вышесказанного уравнение (1.32) примет вид:
(1.33)
Или окончательно
(1.34)
В частном случае, когда из всех массовых сил на движущуюся жидкость действуют только силы тяжести, силовая функция будет равна
(1.35)
Подставив значение силовой функции в уравнение (6) и проинтегрировав, получим уравнение для рассматриваемого сечения: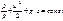 
(1.36)
Так как сумма трех членов в уравнении (8) постоянна для любого сечения струйки, то для двух сечений 1 - 1 и 2 - 2 (рис. 1.15) можно записать
(1.37)
Рис. 1.15
|
Разделив левую и правую часть уравнения (1.37) на g, окончательно получим:
(1.38)
Уравнение (10) устанавливает связь между скоростью движения, давлением и геометрическим положением частиц жидкости для двух сечений струйки и является уравнением Бернулли для элементарной струйки идеальной жидкости