 |
|
Общие свойства алгоритмов, разрешимость и вычислимость.
- Результативность означает возможность получения результата после выполнения конечного количества операций.
- Определенность состоит в совпадении получаемых результатов независимо от пользователя и применяемых технических средств.
- Массовость заключается в возможности применения алгоритма к целому классу однотипных задач, различающихся конкретными значениями исходных данных.
- Дискретность — возможность расчленения процесса вычислений, предписанных алгоритмом, на отдельные этапы, возможность выделения участков программы с определенной структурой.
В математической логике и теории алгоритмов под разрешимостью подразумевают свойство формальной теории обладать алгоритмом, определяющим по данной формуле, выводима она из множества аксиом данной теории или нет. Теория называется разрешимой, если такой алгоритм существует, и неразрешимой, в противном случае.
Функция f с натуральными аргументами и значениями называется вычислимой, если существует алгоритм, ее вычисляющий, то есть такой алгоритм A, что
· если f(n) определено для некоторого натурального n, то алгоритм A останавливается на входе n и печатает f(n);
· если f(n) не определено, то алгоритм A не останавливается на входе
Множество натуральных чисел X называется разрешимым, если существует алгоритм, который по любому натуральному n определяет, принадлежит ли оно множеству X.
Множество натуральных чисел называется перечислимым, если оно перечисляется некоторым алгоритмом, то есть если существует алгоритм, который печатает (в произвольном порядке и с произвольными промежутками времени) все элементы этого множества и только их.
2.1)Интерпретация логических формул, элементарные формулы.
Термом будем называть выражение, образованное из переменных и констант, возможно, с применением функций, а точнее:
1. всякая переменная или константа есть терм;
2. если t1,...,tn — термы, а f — n-местный функциональный символ,то f(t1,...,tn) — терм;
3. других термов нет.
По сути дела, все объекты в программе на Прологе представляются именно в виде термов.
Если терм не содержит переменных, то он называется основным или константным термом.
Атомная или элементарная формула получается путем применения предиката к термам, точнее, это выражение p(t1,...,tn), где p — n-местный предикатный символ, а t1,...,tn — термы.
Формулы логики первого порядка получаются следующим образом:
1. всякая атомная формула есть формула;
2. если A и B — формулы, а x — переменная, то выражения A (читается "не A" или "отрицание A"), A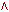 
B (читается "A и B"), A 
B (читается "A или B"), A 
B (читается "A влечет B"), 
хA (читается "для некоторого x" или "существует x") и 
xA (читается "для любого x" или "для всякого x")– формулы;
3. других формул нет.
Высказывание, не допускающее расчленения на более простые, называется элементарным. Для обозначения элементарных высказываний принято использовать символы x, y, z,… в виде строчных букв латинского алфавита, которые в логике называют пропозициональными переменными. Составные высказывания строятся из элементарных с использованием пяти логических связок: отрицание, конъюнкция, дизъюнкция, импликация, эквивалентность.
Семантика формул определяется их свойством быть истинными или ложными, то есть принимать значение T (true) - истина, или F(false) - ложь.
Интерпретировать формулу логики высказываний, значит приписать значения истинности составляющим ее элементарным высказываниям и вычислить истинностное значение всей формулы.
2.2)Истинность формул исчисления предикатов, о доказуемости теорем.
Формула является тождественно истинной, если она истинна при любых значениях входящих в неё переменных.
Язык логики первого порядка строится на основе сигнатуры, состоящей из множества функциональных символов 
и множества предикатных символов 
. С каждым функциональным и предикатным символом связана арность, то есть число возможных аргументов. Допускаются как функциональные так и предикатные символы арности 0. Первые иногда выделяют в отдельное множество констант. Кроме того используются следующие дополнительные символы
· Символы переменных (обычно x,y,z,x1,y1,z1,x2,y2,z2, и т. д.),
· Пропозициональные связки: 
,
· Кванторы: всеобщности 
и существования 
,
· Служебные символы: скобки и запятая.
Перечисленные символы вместе с символами из 
и 
образуют Алфавит логики первого порядка. Более сложные конструкции определяются индуктивно:
· Терм есть символ переменной, либо имеет вид 
, где f — функциональный символ арности n, а 
— термы.
· Атом имеет вид 
, где p — предикатный символ арности n, а 
— термы.
· Формула — это либо атом, либо одна из следующих конструкций: 
, где F,F1,F2 — формулы, а x — переменная.
Переменная x называется связанной в формуле F, если F имеет вид 
либо 
, или же представима в одной из форм 
, причем x уже связанна в H, F1 и F2. Если x не связанна в F, ее называют свободной в F. Формулу без свободных переменных называют замкнутой формулой, или предложением. Теорией первого порядка называют любое множество предложений.
Система логических аксиом логики первого порядка состоит из аксиом исчисления высказываний дополненной двумя новыми аксиомами:
· 
,
· 
,
где A[t / x] — формула, полученная в результате подстановки терма t вместо переменной x в формуле A.
Правил вывода 2:
· Modus ponens: 
· Правило обобщения (GEN): 
Доказательством или выводом формулы F из множества формул Г называется такая конечная последовательность В1, В2 ..., Bs формул, каждая формула которой является либо аксиомой, либо формулой из Г, либо получена из двух предыдущих формул этой последовательности по правилу МР, а последняя формула Bs совпадает с F (Bs = F).
2.3)Преобразование формул без потери истинности, этапы преобразования.
Дизъюнкт — это дизъюнкция конечного числа литералов. Если дизъюнкт не содержит литералов, его называют пустым дизъюнктом и обозначают посредством символа ℵ.
Говорят, что формула находится в конъюнктивной нормальной форме,если это конъюнкция конечного числа дизъюнктов. Имеет место теорема о том, что для любой бескванторной формулы существует формула, логически эквивалентная исходной и находящаяся в конъюнктивной нормальной форме.
Формула находится в предваренной (или префиксной) нормальной форме, если она представлена в виде Q1x1,...,QnxnA, где Qi — это квантор 
или 
, а формула A не содержит кванторов. Выражение Q1x1,...,Qnxn называют префиксом, а формулу A — матрицей.
Формула находится в сколемовской нормальной форме, если она находится в предваренной нормальной форме и не содержит кванторов существования.