 |
|
Никаких других формул в алгебре логики нет.
В качестве примера рассмотрим высказывание "Если я куплю яблоки или абрикосы, то приготовлю фруктовый пирог". Это высказывание формализуется в виде (A v B)  C.
C.
Как показывает анализ формулы (A v B)  C, при определённых сочетаниях значений переменных A, B и C она принимает значение "истина", а при некоторых других сочетаниях — значение "ложь" (разберите самостоятельно эти случаи). Такие формулы называются выполнимыми.
C, при определённых сочетаниях значений переменных A, B и C она принимает значение "истина", а при некоторых других сочетаниях — значение "ложь" (разберите самостоятельно эти случаи). Такие формулы называются выполнимыми.
Некоторые формулы принимают значение "истина" при любых значениях истинности входящих в них переменных. Таковой будет, например, формула А v  , соответствующая высказыванию "Этот треугольник прямоугольный или косоугольный". Эта формула истинна и тогда, когда треугольник прямоугольный, и тогда, когда треугольник не прямоугольный. Такие формулы называются тождественно истинными формулами или тавтологиями. Высказывания, которые формализуются тавтологиями, называются логически истинными высказываниями.
, соответствующая высказыванию "Этот треугольник прямоугольный или косоугольный". Эта формула истинна и тогда, когда треугольник прямоугольный, и тогда, когда треугольник не прямоугольный. Такие формулы называются тождественно истинными формулами или тавтологиями. Высказывания, которые формализуются тавтологиями, называются логически истинными высказываниями.
В качестве другого примера рассмотрим формулу А *  , которой соответствует, например, высказывание "Катя самая высокая девочка в классе, и в классе есть девочки выше Кати". Очевидно, что эта формула ложна, так как либо А, либо
, которой соответствует, например, высказывание "Катя самая высокая девочка в классе, и в классе есть девочки выше Кати". Очевидно, что эта формула ложна, так как либо А, либо  обязательно ложно. Такие формулы называются тождественно ложными формулами или противоречиями. Высказывания, которые формализуются противоречиями, называются логически ложными высказываниями.
обязательно ложно. Такие формулы называются тождественно ложными формулами или противоречиями. Высказывания, которые формализуются противоречиями, называются логически ложными высказываниями.
Если две формулы А и В одновременно, то есть при одинаковых наборах значений входящих в них переменных, принимают одинаковые значения, то они называются равносильными.
Равносильность двух формул алгебры логики обозначается символом "=" или символом "  " Замена формулы другой, ей равносильной, называется равносильным преобразованием данной формулы.
" Замена формулы другой, ей равносильной, называется равносильным преобразованием данной формулы.
Основные законы алгебры логики
В алгебре логики выполняются следующие основные законы, позволяющие производить тождественные преобразования логических выражений (табл. 8.6):
Основные законы алгебры логики
Таблица 8. 6
| Закон | Для ИЛИ | Для И |
| Переместительный | 
| 
|
| Сочетательный | 
| 
|
| Распределительный | 
| 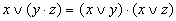
|
| Правила де Моргана | 
| 
|
| Идемпотенции | 
| 
|
| Поглощения | 
| 
|
| Склеивания | 
| 
|
| Операция переменной с ее инверсией | 
| 
|
| Операция с константами | 
| 
|
| Двойного отрицания | 
|
Таблицы истинности
Таблица истинности логической формулы выражает соответствие между всевозможными наборами значений переменных и значениями формулы.
Для формулы, которая содержит две переменные, таких наборов значений переменных всего 22 - четыре: (0, 0), (0, 1), (1, 0), (1, 1).
Если формула содержит три переменные, то возможных наборов значений переменных 23 - восемь: (0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1).
Количество наборов для формулы с четырьмя переменными равно шестнадцати и т.д.
Удобной формой записи при нахождении значений формулы является таблица, содержащая кроме значений переменных и значений формулы также и значения промежуточных формул.
Пример 1
Составьте таблицу истинности для формулы  , которая содержит две переменные x и y. В двух первых столбцах таблицы запишите четыре возможных пары значений этих переменных, в последующих столбцах — значения промежуточных формул и в последнем столбце — значение формулы. В результате получите таблицу 8.7:
, которая содержит две переменные x и y. В двух первых столбцах таблицы запишите четыре возможных пары значений этих переменных, в последующих столбцах — значения промежуточных формул и в последнем столбце — значение формулы. В результате получите таблицу 8.7:
Таблица истинности для примера 1
Таблица 8. 7
| Переменные | Промежуточные логические формулы | Формула | |||||
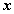
| 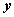
| 
| 
| 
| 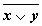
| 
| 
|
Из таблицы видно, что при всех наборах значенийпеременныхxиyформула  принимает значение 1, то есть является тождественно истинной.
принимает значение 1, то есть является тождественно истинной.
Пример 2
Таблица истинности для формулы  приведена в табл. 8.8:
приведена в табл. 8.8:
Таблица истинности для примера 2
Таблица 8. 8
| Переменные | Промежуточные логические формулы | Формула | ||||
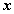
| 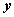
| 
| 
| 
| 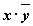
| 
|
Из таблицы видно, что при всех наборах значенийпеременныхxиy
формула  принимает значение 0, то есть является тождественно ложной.
принимает значение 0, то есть является тождественно ложной.
Пример 3
Таблица истинности для формулы  приведена в табл. 8.9:
приведена в табл. 8.9:
Таблица истинности для примера 3
Таблица 8. 9
| Переменные | Промежуточные логические формулы | Формула | ||||||
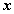
| 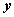
| 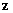
| 
| 
| 
| 
| 
| 
|
Из таблицы видно, что формула  в некоторых случаях принимает значение 1, а в некоторых — 0, то есть является выполнимой.
в некоторых случаях принимает значение 1, а в некоторых — 0, то есть является выполнимой.