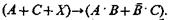 |
|
Восстановление булевой функции по изображающему числу
Рассмотрим методы, позволяющие переходить от задания булевой функции в виде изображающего числа к явному выражению ее через элементы.
Дизъюнктивная нормальная форма (ДНФ). Пусть имеется множество, состоящее из n элементов А1 ..., Аn. Произведение вида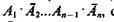 
доставленное из элементов Ai или их отрицаний Aj и содержащее n сомножителей, называется элементарным произведением. Из n элементов можно составить 2n различных элементарных произведений. Изображающее число каждого элементарного произведения имеет только одну единицу в одном из 2n разрядов. Например, выпишем для трех высказываний А, В, С все возможные элементарные произведения и их изображающие числа по отношению к b [А, В, С]:
Совершенная дизъюнктивная нормальная форма (СДНФ) булевой функции — сумма элементарных произведений. Чтобы по данному изображающему числу восстановить булеву функцию в СДНФ, нужно суммировать элементарные произведения, изображающие числа которых имеют единицы в тех же разрядах, что и изображающее число булевой функции. Например, 1001 0110 имеет единицы в разрядах 0, 3, 5, 6, поэтому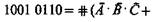 
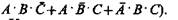
Конъюнктивная нормальная форма (КНФ). Элементарными суммами для лnэлементов А1 ..., Аn называются суммы вида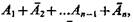 
составленные из элементов Аi A`или их отрицаний j и содержание n слагаемых. Из n элементов можно составить 2n элементарных сумм. Изображающие числа элементарных сумм содержат только один 0 в одном из 2 n разрядов. Например, для трех высказываний А, В, С имеем
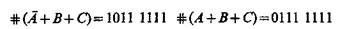
Конъюнктивная нормальная форма булевой функции представляет собой произведение элементарных сумм. Для того чтобы написать булеву функцию, соответствующую данному изображающему числу в КНФ, необходимо перемножить элементарные суммы, изображающие числа которых имеют те же 0, что и изображающее число булевой функции. Например, число 1001 0110 имеет 0 в разрядах 1, 2, 4 и 7, поэтому 1001 0110 =
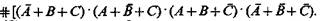
Булевы уравнения
Решение многих задач, связанных с распознаванием образов, может быть сведено к решению булевых алгебраических уравнений с одним (или более) неизвестными. Примером булева уравнения с одним неизвестным может служить соотношение X&(A+B)≡A&B&C, где X — некоторая булева функция, зависящая от А, В,С, такая, чтобы в результате подстановки Х(А, В, С) в уравнение оно обращалось в тавтологию.
Перейдем от элементов X, А, В, С к их изображающим числам. Относительно базиса b [А, В, С] найдем #А=00000001; #(A+B)=01110111 и, следовательно, #Х должно быть таким, чтобы выполнялось равенство
#X&(0111 0111) ≡00000001.
Представим #X=(x0x1x2x3x4x5x6x7x8).
Для каждой компоненты этого вектора получим отдельное уравнение, беря исходные данные построчно:
Отсюда находим:
x0&0=0. Поскольку любое из чисел в конъюнкции с нулём даст 0, то x0 может быть любым, и мы будем обозначать это, как x0=*.
Далее, x1&1=0. Только x1=0 может дать такой результат. Аналогичное решение получается для x2, x3, x5 и x6. Решение для x4 получается так же, как и для x0, а в случае x7 мы будем иметь x7&1=1, откуда x7=1.
Общее решение уравнения запишем в виде изображающего числа X:
#X=[*000*001].
Таким образом, рассматриваемое уравнение имеет четыре решения, соответствующие изображающим числам 0000 0001, 00001001, 10000001 и 10001001, которым соответствуют 4 логических функции
,
,
,
.
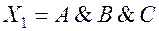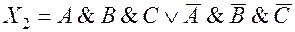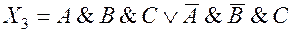(здесь мы вернулись к общепринятым обозначениям дизъюнкции и конъюнкции).
Аналогично можно найти решение уравнения в виде импликации, например
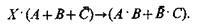
Уравнение в виде импликации всегда можно записать как соотношение эквивалентности, например, вместо приведённого выше уравнения можно было бы написать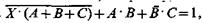 
или после упрощения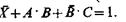 
Существуют также уравнения, которые вообще не имеют решений, например 