Дискретизація рівняння

Стр 1 из 2Следующая ⇒

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

Національний університет «Львівська політехніка»

Диференціальні рівняння

з частинними похідними.

Метод сіток

ЗАВДАННЯ ТА МЕТОДИЧНІ РЕКОМЕНДАЦІЇ

до лабораторної роботи № 11

з курсу «Чисельні методи»

для базового напрямку 040204 «Прикладна фізика»

Затверджено

на засіданні кафедри

обчислювальної математики та програмування

Протокол № 5 від 30.01.2012 p.

ЛЬВІВ – 2011

Диференціальні рівняння з частинними похідними. Метод сіток.Завдання та методичні рекомендації до лабораторної роботи № 11 з курсу «Чисельні методи» для базового напрямку 040204 «Прикладна фізика» / Укл. Я.М.Глинський, Н.М.Гоблик, З.О.Гошко, В.А.Ряжська, 2012. – 19 с.

Укладачі: Глинський Я.М., канд. фіз.-мат. наук, доц.

Гоблик Н.М., ст. викл.

Гошко З.О., асистент

Ряжська В.А., канд. фіз.-мат. наук, доц.

Відповідальна за випускРяжська В.А., канд. фіз.-мат. наук, доц.

Рецензентдоктор фіз.-мат. наук, проф. Чабанюк Я.М.

Передмова

У методичних вказівках розглянуто методи розв’язування диференціальних рівнянь в частинних похідних, які задовольняють початковим умовам.

Методичні вказівки містять короткі теоретичні відомості, приклади розв’язування крайових задач еліптичного, параболічного та гіперболічного типів для диференціальних рівнянь в частинних похідних за допомогою методу сіток (методу скінченних різниць), а також індивідуальні завдання для самостійної роботи студентів. Приклади розв’язані як вручну, так і у середовищі MatLab

Методичні вказівки призначені для студентів базового напрямку 040204 «Прикладна фізика» і укладені відповідно до робочої програми курсу «Чисельні методи».

1. МЕТА РОБОТИ

Мета роботи – навчитись знаходити розв’язок диференціального рівняння в частинних похідних, яке задовольняє початковим умовам, за допомогою методу сіток (методу скінченних різниць).

2. ТЕОРЕТИЧНІ ВІДОМОСТІ

Диференціальне рівняння в частинних похідних другого порядку з двома незалежними змінними в загальному випадку має вигляд

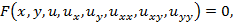
де – незалежні змінні, – шукана функція, – частинні похідні.

Рівняння першого степеня щодо шуканої функції і всіх її похідних, яке не містить їх добутків, називають лінійним. Таке рівняння можна записати у вигляді

де коефіцієнти можуть залежати лише від х та у.

Якщо коефіцієнти не залежать від х та у, то таке рівняння називають лінійним диференціальним рівнянням з постійними коефіцієнтами.

Для повного опису фізичного процесу потрібно крім самого рівняння з частинними похідними задати початковий стан процесу (початкові умови) і режим на границі області (граничні умови). Початкові та граничні умови дають змогу визначити єдиний розв’язок диференціального рівняння.

Розрізняють три типи лінійних диференціальних рівнянь:

· еліптичного типу ( );

· параболічного типу ( );

· гіперболічного типу ( ).

Відшукання розв’язку лінійного диференціального рівняння в частинних похідних методом сіток можна поділити на декілька етапів:

· дискретизація області (побудова сітки);

· дискретизація рівняння (заміна частинних похідних їх скінченними різницями);

· дискретизація граничних і початкових умов;

· визначення значення функції у вузлах сітки.

Побудова сітки

Розглянемо один із простіших способів побудови сітки.

Нехай на площині є деяка область W з границею Г. Побудуємо на площині дві сім’ї паралельних прямих

точки перетину цих прямих називають вузлами сітки.

Два вузли називають сусідніми, якщо вони віддалені один від одного на відстань кроку у відповідному напрямку. Сукупність сусідніх з вузлом вузлів

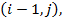
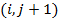
утворюють п’ятиточкову зірку з центром в точці

Вузол називають внутрішнім вузлом, якщо всі вузли його зірки лежать в області W + Г.

Вузол називають граничним вузлом, якщо хоча б один із вузлів зірки не належить області W + Г.

Значення шуканої функції у вузлах сітки позначатимемо .

Дискретизація рівняння

В кожному внутрішньому вузлі замінимо частинні похідні скінченними різницями, тобто

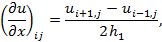
В граничних точках слід використовувати формули

Задача Діріхле

Нехай задано рівняння Пуассона

яке на межі області задовольняє граничні умови

Таку крайову задачу називають задачею Діріхле.

Побудувавши сітку Нехай Замінивши частинні похідні скінченними різницями, отримаємо рівняння

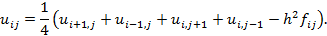
Підставляючи в це рівняння конкретні значення i, j отримаємо систему лінійних алгебраїчних рівнянь, яку розв’язуємо одним із відомих методів.

Якщо , то таке рівняння називають рівнянням Лапласа.

Приклад 1. Розв’язати граничну задачу

u₁₂

u₂₂

u₃₂

u₄₂

u₂₀

u₃₀

u₄₀

u₀₁

u₁₁

u₂₁

u₃₁

u₄₁

u₁₃

u₂₃

u₃₃

u₄₃

u₀₄

u₁₄

u₂₄

u₃₄

u₄₄

u₀₂

u₀₀

0 0,25 0,5 0,75 1 x

y 0,75 0,5 0,25

u₁₀

u₀₃

Розв’язування. Маємо

Нехай

Проведемо дискретизацію області та порахуємо значення функції в граничних вузлах. З граничної умови

отримаємо

, , , , ;

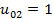з граничної умови будемо мати

, ,

, , ;

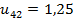з граничної умови будемо мати

, , , , ;

з останньої граничної умови :

, , , , .

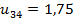Значення у внутрішніх вузлах визначимо за формулою

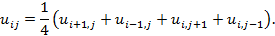
Отже,

Складемо систему з дев’яти рівнянь. Отримаємо

Розв’язавши систему, отримаємо

, , ,

, , .

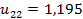Отже, розв’язком даної задачі буде (значення функції у вузлах сітки)

12 Следующая ⇒