 |
|
Задача теплопровідності
Розглянемо рівняння параболічного типу
яке задовольняє початкову умову
та граничні умови
,
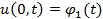, де 
Класичним прикладом такої задачі є задача теплопровідності або дифузії.
Зауваження. Якщо зробити заміну 
то отримаємо рівняння
яке і розглядатимемо далі.
Побудуємо сітку 
та дискретизуємо початкову та граничні умови. Отримаємо
, 
, 
.
| (i+1,j) |
| (i-1,j) |
| (i,j) |
| (i,j+1) |
Тоді
Побудовану схему називають явною скінчено-різницевою схемою.
Зауваження. Для того, щоб явна скінченно-різницева схема була стійка та збігалась до розв’язку необхідно, щоб для вибраних кроків виконувались нерівності
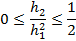
| (i+1,j) |
| (i-1,j) |
| (i,j-1) |
| (i,j) |
Тоді
Таку схему називають неявною скінчено-різницевою схемою.
Якщо вибрати кроки так, щоб 
, то у випадку явної схеми будемо мати
а у випадку неявної –
Якщо для явної схеми вибрати 
, то отримаємо
Приклад 2. Розв’язати рівняння методом сіток
,
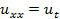Розв’язання. Виберемо крок по осі х 
і нехай
Отже,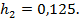 
Тоді скінченно-різницеве рівняння буде мати вигляд
Порахуємо значення функції в граничних вузлах.
З початкової умови 
будемо мати
З граничної умови 
отримаємо
, 
, 
, 
, 
;
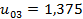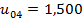a з граничної умови 
будемо мати
, 
,
Обчислимо внутрішні значення
Результати обчислень значення функції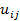 
занесемо в таблицю:
| i | ||||||
| j | xi tj | 0,0 | 0,5 | 1,0 | 1,5 | 2,0 |
| 0,000 | 1,000 | 1,000 | 1,000 | 1,000 | 1,000 | |
| 0,125 | 1,125 | 1,000 | 1,000 | 1,000 | 1,125 | |
| 0,250 | 1,250 | 
| 1,000 |
| 1,250 | |
| 0,375 | 1,375 | 1,125 | 1,063 | 1,125 | 1,375 | |
| 0,500 | 1,500 | 1,219 | 1,125 | 1,219 | 1,500 |
Розв’язана гранична задача описує розподіл температури в однорідному стержні довжиною 2, а отримані результати - характер охолодження стержня з бігом часу.
Розв’язання в середовищі MATLAB
Програма розв’язування рівняння теплопровідності складається з 4-х файлів:
1)файл m_sitok.m
function u=m_sitok(a,b,t0,tk,h1,h2,f1,f2,tau)
%розв'язування рівняння теплопровідності (метод сіток -явна
%скінчено-різнецева схема)
%a -початкове значення х
%b - кінцеве значення х
%t0 - початкове значення t
%tk - кінцеве значення t
%h1- крок по x
%h2 - крок по t
%f1 -гранична умова в точці а (рядкова змінна -ім'я файл-функції)
%f2-гранична умова в точці b(рядкова змінна -ім'я файл-функції)
%tau - початкова умова (рядкова змінна -ім'я файл-функції)
if h2/h1^2>0.5
error('Не виконуються умови збіжності, змініть крок')
end
x=a:h1:b;
t=t0:h2:tk;
J=length(x);
N=length(t);
u=zeros(N,J);
%обчислення значень функції в граничних вузлах
for k=1:J
u(1,k)=feval(tau,x(k));
end
for k=1:N
u(k,1)=feval(f1,t(k));
u(k,J)=feval(f2,t(k));
end
%обчислення значень функції у внутрішніх вузлах
s=h2/h1^2;
for k=1:N-1
u(k+1,2:J-1)= s*(u(k,3:J)+u(k,1:J-2))+(1-2*s)*u(k,2:J-1);
end
2)файл f1.m – функція, яка описує граничну умову при x=a
function y=f1(t)
y=t+1;
3)файл f2.m – функція, яка описує граничну умову при x=b
function y=f2(t)
y=t+1;
4)файл tau.m– функція, яка описує початкову умову
function y=tau(x)
y=1;
Виклик програми:
>> h1=0.5;
>> h2=0.125;
>> a=0;
>> b=2;
>> t0=0;
>> tk=0.5;
>> u=m_sitok(a,b,t0,tk,h1,h2,'f1','f2','tau')
u =
1.0000 1.0000 1.0000 1.0000 1.0000
1.1250 1.0000 1.0000 1.0000 1.1250
1.2500 1.0625 1.0000 1.0625 1.2500
1.3750 1.1250 1.0625 1.1250 1.3750
1.5000 1.2188 1.1250 1.2188 1.5000
Хвильове рівняння
Розглянемо рівняння гіперболічного типу
яке задовольняє початкові умови
, 
та граничні умови
,
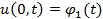, де
Класичним прикладом такої задачі є задача коливання струни довжиною 
, з рухомими кінцями, для якої відомий її стан в початковий момент часу 
.
Зауваження. Якщо зробити заміну то отримаємо рівняння
яке і розглядатимемо далі.
Виберемо крок по 
та по 
і побудуємо сітку Дискретизуємо початкові та граничні умови. Отримаємо
, 
,
, .
Замінимо в заданому рівнянні частинні похідні скінченними різницями. Отримаємо рівняння
Звідси
Побудовану схему називають явною скінчено-різницевою схемою.
Зауваження. Для того, щоб різницева схема була стійка та збігалась до розв’язку необхідно, щоб для вибраних кроків виконувались нерівності
Якщо вибрати кроки так, щоб 
, то будемо мати
Приклад 3. Методом сіток розв’язати рівняння
,
Розв’язання. Виберемо рівні кроки 
.
Тоді скінченно-різницеве рівняння буде мати вигляд
Порахуємо значення функції в граничних вузлах.
З початкової умови 
будемо мати (значення першого рядка таблиці)
Дискретизуємо другу початкову умову:
З останньої формули будемо мати (значення першого рядка таблиці)
З граничної умови 
отримаємо (значення першого стовпця таблиці)
, 
, 
, 
, 
;
a з граничної умови 
будемо мати (значення останнього стовпця таблиці)
, 
,
Обчислимо значення функції у внутрішніх вузлах. Значення третього рядка таблиці:
Обчислимо значення четвертого рядка таблиці
Аналогічно обчислюємо значення в наступних рядках.
Результати обчислень значення функції 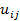занесемо в таблицю:
| i | ||||||
| j | xi tj | 0,00 | 0,25 | 0,50 | 0,75 | 1,0 |
| 0,00 | 0,00 | 0,25 | 0,50 | 0,75 | 1,00 | |
| 0, 25 | 0,25 | 0,00 | 0,75 | 0,50 | 1,25 | |
| 0,50 | 0,50 | 
| 0,00 | 
| 1,50 | |
| 0,75 | 0,75 | 0,50 | 1,25 | 1,00 | 1,75 | |
| 1,00 | 1, 00 | 1,25 | 1,50 | 1,75 | 2,00 |
Розв’язання в середовищі MATLAB
Програма розв'язування хвильового рівняння складається з 5-и файлів:
1) файл m_sitok2.m
function u=m_sitok2(a,b,t0,tk,h1,h2,f1,f2,tau,tau1)
%розв'язування хвильового рівняння (метод сіток -явна
%скінчено-різнецева схема)
%a -початкове значення х
%b - кінцеве значення х
%t0 - початкове значення t
%tk - кінцеве значення t
%h1- крок по x
%h2 - крок по t
%f1 -гранична умова в точці а (рядкова змінна -ім'я файл-функції)
%f2-гранична умова в точці b(рядкова змінна -ім'я файл-функції)
%tau - початкова умова (рядкова змінна -ім'я файл-функції)
%tau1 - початкова умова - похіднa шуканої функції за змінною t(рядкова змінна -ім'я файл-функції)
if (h2/h1)^2>1
error('Не виконуються умови збіжності, змініть крок')
end
x=a:h1:b;
t=t0:h2:tk;
J=length(x);
N=length(t);
u=zeros(N,J);
%обчислення значень функції в граничних вузлах
for k=1:J
u(1,k)=x(k);
end
for k=1:J
u(2,k)=u(1,k)+h2*feval(tau1,k-1);
end
for k=3:N
u(k,1)=feval(f1,t(k));
u(k,J)=feval(f2,t(k));
end
%обчислення значень функції у внутрішніх вузлах
s=(h2/h1)^2;
for k=3:N
u(k,2:J-1)= s*(u(k-1,3:J)+u(k-1,1:J-2))+2*(1-s)*u(k-1,2:J-1)-u(k-2,2:J-1) ;
end
2) файл f1.m – функція, яка описує граничну умову при x=a
function y=f1(t)
y=t;
3) файл f2.m – функція, яка описує граничну умову при x=b
function y=f2(t)
y=t+1;
4) файл tau.m– функція, яка описує початкову умову
function y=tau(x)
y=x;
5) файл tau1.m – функція, яка описує початкову умову – похідну шуканої функції за змінною t
function y=tau1(x)
y=cos(pi*x);
Виклик програми:
>> a=0;
>> b=1;
>> t0=0;
>> tk=1;
>> h1=0.25;
>> h2=0.25;
>> u=m_sitok2(a,b,t0,tk,h1,h2,'f1','f2','tau','tau1')
u =
u =
0 0.2500 0.5000 0.7500 1.0000
0.2500 0 0.7500 0.5000 1.2500
0.5000 0.7500 0 1.2500 1.5000
0.7500 0.5000 1.2500 1.0000 1.7500
1.0000 1.2500 1.5000 1.7500 2.0000