 |
|
Начальное приближение.
В качестве начальных данных возьмём γ, α. Находим указанными в предыдущем пункте методами 
, 
, 
, 
.
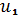Чтобы найти 
, надо воспользоваться начальным приближением. Но прежде необходимо составить функцию F( )=0.
Из (15.4) выразим 
, так как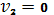 
, через 
и получим 
. Подставив его в (15.3), получим уравнение, зависящее только от и :
(*)
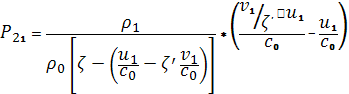Но если воспользоваться уравнением (4.3), которое является уравнением (15.1), разрешённым относительно
то получим:
(**)
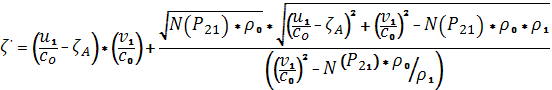, так как 
.
Осталось найти 
. Это можно сделать по формулам (2.1), (2.2), (2.3) и (2.4):
(***)
, так как:
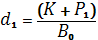(2.1), 
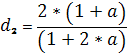(2.2), 
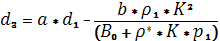(2.3)
, так как 
.
Если же теперь подставим уравнение (***) в уравнение (**), а получившееся уравнение в уравнение (*), то получим, очевидно, уравнение, зависящее только от .Теперь нам стало видно, насколько полезно использование функций и подфункций при работе с ЭВМ. Если теперь раскрыть замену 
, заметив, что 
, то получим уравнение лишь с одной неизвестной - 
. Её-то нам и необходимо приблизить.
Приближать будем методом касательных. Ниже приведён алгоритм на языке Python:
import math
import string
def g(x):
return # "Требуемая функция"
def differ(x):
return float((g(x+0.001)-g(x))/0.001)
def Newton():
x0=#"Начальное приближение"
x1=x0-(g(x0)/differ(x0))
while math.fabs(x1-x0)>0.01:
x2=x1-(g(x1)/differ(x1))
x0=x1
x1=x2
return x1
, где "Требуемая функция" есть ни что иное как искомая функция от .
Осталось выбрать начальное приближение. В этом нам поможет график:
Теперь, использовав метод касательных и получив точное значение , последовательно находим и . Подставляем в уравнение (***) , а затем полученный результат в уравнение (**) и находим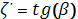 
.
Тогда из (15.4) найдём , а из (15.2) найдём 
. То есть все величины найдены и наша задача выполнена.
[1] Шиндяпин Г.П. Математическое моделирование в задачах динамики многофазных сред. Часть I: нелинейные локальные взаимодействия ударных волн. Саратов, 1988г.