 |
|
УРАВНЕНИЕ БЕГУЩЕЙ ВОЛНЫ
Получим уравнение плоской волны в однородной среде вдоль оси 0х, совпадающей с направлением её распространения. Т.к., в этом случае фронт волны перпендикулярен 0х, то смещения s частиц среды будут зависеть только от координаты х и момента времени t, т.е. уравнение волны будет представлять собой функцию – s = f(x,t). Пред-положим, что в точке 0 (рис.1) частица совершает колебания по гармоническому закону: s = Acosωt. Тогда, очевидно, что колебания в некоторой точке М, удаленной от точки 0 на расстояние 0М = х, будут совершаться по тому же закону, но с некоторым отставанием по времени τ от колебаний в точке 0:
s = A cosω(t-τ) (1)
Если обозначить скорость волны через u, то время запаздывания, за которое волна добежит от точки 0 до точки М: τ = х/u, и уравнение колебаний в произвольной точке М на расстоянии х от источника примет вид:
s= A cos ω( t-τ ) = A cos ω( t - 
). (2)
Это и есть искомое уравнение плоской бегущей волны. Здесь: А – амплитуда смещения частиц среды от положения равновесия, ω – циклическая частота колебаний частиц, ω( t - ) – фаза колебаний в точке с координатой х, u – скорость плоской волны.
Расстояние между ближайшими частицами среды, колеблющимися в одинаковой фазе, называется длиной волны λ (рис.1).
Длина волны равна расстоянию, на которое распространяется определенная фаза колебаний за период колебаний частиц среды. Тогда λ = u·T = u/ν. Т.к. ω = 2πν, то (2) можно переписать в виде:
s = Acosω( t -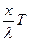 
) = Acos2π(vt - 
) = Acos(ωt - 2π ). (3)
Покажем, что скорость распространения волны u – это скорость перемещения фиксированного значения фазы. Положим ω( t – ) = С, т.е. const. Выразим х: х = ut - Cu/ω. Продифференцировав это выражение по t, получим: 
(С, u, ω – величины постоянные для данной среды). Т.е. u – это скорость, с которой перемещается данное значение фазы. По этой причине скорость волны называют также фазовой скоростью.
Скорость распространения механических волн зависит от физических свойств среды. Скорость распространения продольных волн определяется формулой: 
. Для поперечных волн – 
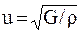. Здесь r – плотность недеформированной среды, Е – модуль Юнга, G – модуль сдвига. Е и G – параметры упругости среды.
Основные свойства волн: прямолинейность распространения в однородной среде, отражение и преломление на границе раздела сред, дисперсия, интерференция и дифракция.
ВОЛНОВОЕ УРАВНЕНИЕ
Аналогично тому, как уравнение колебаний является решением дифференциального уравнения, описывающего процесс колебаний, так и уравнение волны представляет собой решение дифференциального уравнения, описывающего процесс распространения волн в среде. Это дифференциальное уравнение второго порядка в частных производных называется волновым. Найдем его вид. Запишем первые и вторые производные уравнения волны (2) по переменным t и х:
; 
;
; 
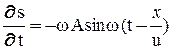; (4)
Откуда:
; 
. (5)
В трехмерном случае:
.
СТОЯЧИЕ ВОЛНЫ
Рассмотрим в качестве примера проявления волновых свойств механизм образования стоячих волн. Они возникают в результате наложения (интерференции) двух встречных плоских когерентных волн с одинаковой амплитудой. Например, волны падающей и этой же волны отраженной от границы раздела сред. Запишем уравнения двух плоских волн, движущихся навстречу друг другу в виде (3).
s 1= Acos(ωt – 2π ) = А(cosωt cos2π + sinωt sin2π ) . (6)
s2 = Acos(ωt + 2π ) = А(cosωt cos2π – sinωt sin2π ). (7)
Складывая эти равенства, получим уравнение результирующего процесса – уравнение стоячей волны:
(8)
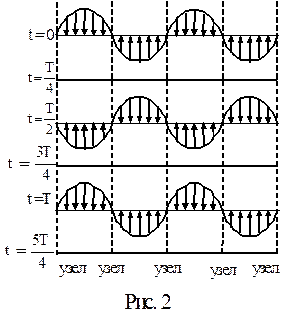Из (8) видно, что в каждой точке среды происходит колебание той же частоты ω, что и у интерферирующих волн. Однако амплитуда колебаний каждой частицы зависит от координаты точки среды, в которой она расположена: Ах = 2А cos2π . В точках, где аргумент 2π = ±nπ (при n = 0, 1, 2…) и |cos2π | = 1, амплитуда имеет максимальное значение –2А. Эти точки называются пучностями стоячей волны. В точках, где аргумент 2π = ±(n +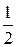 
)π, амплитуда минимальна и равна нулю, т.к. в этом случае cos2π = 0. Эти точки называются узлами стоячей волны.
На рис.2 показано как меняется расположение частиц среды в стоячей волне в течение периода.