 |
|
Обчислення криволінійних інтегралів першого роду
Формула (4), яка зводить криволінійний інтеграл до звичайного, є не зовсім зручною для обчислення, бо не завжди можна легко знайти рівняння кривої 
у вигляді 
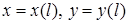, де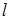 
– довжина дуги. Спростимо цю формулу.
Нехай крива задана рівняннями 
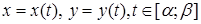, причому значення 
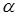відповідає точці 
, а значення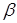 
– точці 
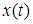. Вважатимемо, що функції 
і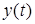 
разом з похідними 
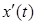і 
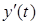неперервні на відрізку 
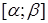, а функція 
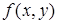неперервна вздовж кривої . Для довільної точки 
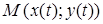довжину дуги 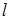кривої 
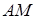можна розглядати як функцію параметра 
: 
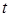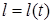, тоді
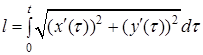
Звідси, згідно з правилом диференціювання визначеного інтеграла по верхній межі, маємо
.
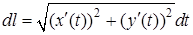Виконуючи заміну змінної 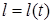у правій частині формули (4), маємо
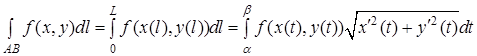(6)
Зокрема, якщо крива в декартових координатах задана рівнянням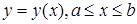 
, де функція 
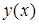неперервна разом із своєю похідною 
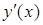на відрізку 
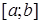, то формула (6) набирає вигляду
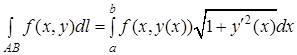(7)
Якщо крива задається рівнянням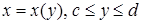 
і функці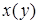ї 
і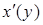 
неперервні на відрізку 
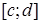, то
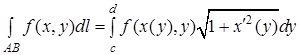(8)
Досі ми вважали, що криволінійний інтеграл першого роду розглядається для плоскої кривої . Знайдені результати легко перенести на випадок просторових кривих.
Нехай функція 
визначена та неперервна на просторовій кривій , яку задано рівняннями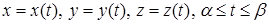 
, де функції 
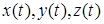та 
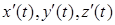неперервні на відрізку 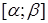. Тоді існує криволінійний інтеграл 
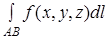і справджується формула
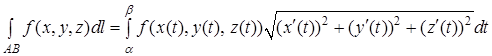. (9)
Приклади
1. Обчислити криволінійний інтеграл
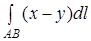
де – відрізок прямої 
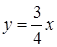від точки 
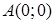до точки 
.
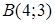Розв’язання
Скористаємося формулою (7). Оскільки
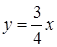, а 
, 
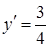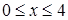, то
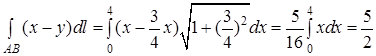
2. Обчислити криволінійний інтеграл першого роду
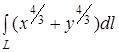
де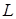 
– астроїда 
.
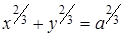Розв’язання
Запишемо параметричні рівняння астроїди:
Оскільки 
, то
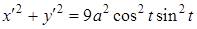
Зазначимо, що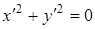 
у точках 
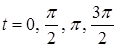, тобто астроїда є кусково-гладкою кривою.
Для обчислення криволінійного інтеграла застосовуємо формулу (6). Отримаємо
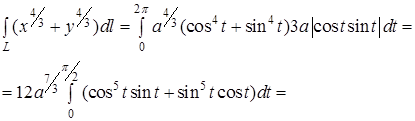
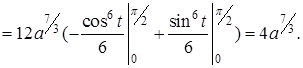
3 Застосування криволінійного інтеграла першого роду
1. Застосування в геометрїї. Нехай у площині 
задано кусково-гладку криву замкнену чи незамкнену і на цій кривій визначено неперервну функцію 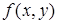, тоді:
а) площу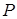 
циліндричної поверхні, визначеної функцією 
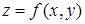, знаходять за формулою
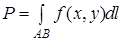(10)
б) довжину 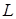кривої визначають за формулою
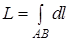(11)
2. Застосування у механіці. Нехай вздовж неоднорідної матеріальної кривої 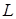розподілено масу з лінійною густиною 
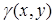, тоді:
а) маса кривої 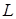обчислюється за формулою
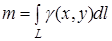(12)
б) координати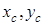 
центра маси кривої 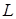знаходяться за формулами
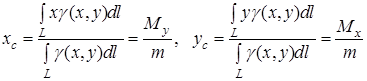(13)
де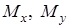 
– статичні моменти кривої 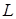відносно осей 
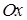і 
;
в) моменти інерції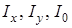 
кривої 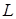відносно осей 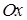, і початку координат відповідно дорівнюють
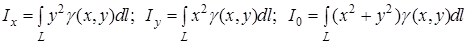(14)
У випадку, коли крива однорідна, тобто має сталу густину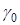 
, у формулах (12) – (14) слід вважати 
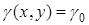. Наприклад, необхідно знайти момент інерції 
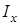відносно осі 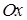однорідної 
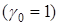дуги кола 
, яка міститься у першій чверті.
Скориставшись першою з формул (14), матимемо
.
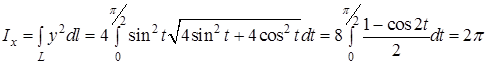Формули (10), (11) випливають з геометричного змісту криволіній-ного інтеграла першого роду (п. 1).
Формули (12) – (14) можна довести тим самим методом, яким були знайдені відповідні формули для матеріальної пластини (п. 1.6).
Формули (11) – (14) можна записати і для випадку, коли підін-тегральна функція розглядається на просторовій кривій.