 |
|
Векторы, операции над ними.
НЕДЕЛЯ 2
Лекция 3.
Координаты точки на прямой и плоскости.
Деление отрезка в данном отношении.
В основе метода координат лежит понятие системы координат.
Две взаимно перпендикулярные оси Ох и Оу, имеющие общее начало О и одинаковую масштабную единицу, образуют прямоугольную систему координат. Ось Ох называется осью абсцисс, ось Оу – осью ординат.
В прямоугольной системе координат Оху точку М, имеющую координаты х и у, обозначают М(х; у), где х – абсцисса точки, а у – её ордината.
Пусть в прямоугольной системе координат заданы точки М1(х1, у1) и М2(х2;у2). Расстояние между ними определяется по формуле:
 (1)
(1)
Три точки плоскости, не лежащие на одной прямой образуют треугольник.
Теорема.Для любых трех точек А(х1;у1),В(х2;у2) и С(х3;у3), не лежащих на одной прямой, площадь S треугольника АВС вычисляется по формуле
 (2)
(2)
Пусть на плоскости дан произвольный отрезок М1М2 и пусть М – любая точка этого отрезка, отличная от точки М2 (рис.1).
Координаты точки М(х;у) делящей отрезок между точками М1(х1;у1) и М2(х2;у2) в заданном отношении λ, определяются по формулам:
 (3)
(3)
При λ=1 получаем формулы для координат середины отрезка:
 (4)
(4)
 |
 у М2(х2;у2)
у М2(х2;у2)
М1(х1;у1) М(х;у) ρ М
φ
О Р1 Р Р2 х O
рис.1 рис.2
В полярной системе координат положение точки М на плоскости определяется её расстоянием |ОМ|=ρ от полюса О (ρ–полярный радиус-вектор точки) и углом φ, образованным отрезком ОМ с полярной осью ОЕ (рис.2). Угол φ считается положительным при отсчете от полярной оси против часовой стрелки.
Прямоугольные координаты х и у точки М и её полярные координаты ρ и φ связаны следующими формулами
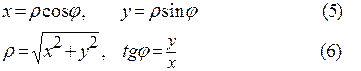
Литература: К,А, Хасеинов Каноны математики. Стр.61-63.
Лекция 4.
Векторы, операции над ними.
Рассмотреть самостоятельно следующие понятия: вектор, длина вектора, нулевой и единичный вектор, равные вектора, коллинеарные и компланарные вектора, сложение и вычитание вектора по правилам треугольника и параллелограмма, умножение вектора на число.
Пусть задана ось L и некоторый вектор АВ. Проекцией вектора АВ на ось L называется величина А¢В¢ на оси L. Проекция вектора АВ на ось L равна длине вектора АВ, умноженной на косинус угла между вектором АВ и осью L, т.е.

Направляющими косинусами вектора `а  называются косинусы углов между вектором `а и осями координат. Направляющие косинусы вектора `а
называются косинусы углов между вектором `а и осями координат. Направляющие косинусы вектора `а  можно определить по формулам
можно определить по формулам

Векторы можно складывать, вычитать и умножать на число.
Определение 1. Суммой 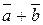 называется вектор, который идет из начала вектора
называется вектор, который идет из начала вектора  в конец вектора
в конец вектора 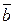 при условий, что вектор
при условий, что вектор 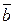 приложен к концу вектора
приложен к концу вектора  .
.
Определение 2. Разностью  векторов
векторов 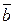 и
и  называется вектор, который в сумме с вектором
называется вектор, который в сумме с вектором  дает вектор
дает вектор 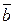 .
.
Определение 3. Произведением 
 называется вектор, который коллинеарен вектору
называется вектор, который коллинеарен вектору  , имеет длину, равную
, имеет длину, равную  и направление такое же, как и вектор
и направление такое же, как и вектор  , если
, если  >0 и противоположное, если
>0 и противоположное, если  <0.
<0.
Пусть даны векторы 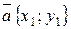 и
и 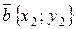 . Тогда сумма векторов в координатной форме записывается
. Тогда сумма векторов в координатной форме записывается
 ,
,
разность векторов
 ,
,
умножение вектора на число l
 .
.
Определение 4. Скалярным произведением двух ненулевых векторов  и
и 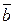 называется число, равное произведению длин этих векторов на косинус угла между ними
называется число, равное произведению длин этих векторов на косинус угла между ними
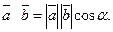
Если векторы  и
и  заданы координатами, то скалярное произведение можно вычислить по формуле
заданы координатами, то скалярное произведение можно вычислить по формуле

Свойства скалярного произведения векторов:
 .
. 
 .
. 
 .
. 
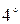 .
. 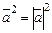
 .
.  , если
, если 
Следствие. Угол между векторами  и
и 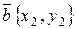 определяется по формуле
определяется по формуле

или

Сформируем условия параллельности перпендикулярности двух векторов  и
и 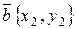
1. Векторы  и
и 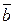 перпендикулярны, если их скалярное произведение равно
перпендикулярны, если их скалярное произведение равно 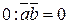 , то есть
, то есть

или

2. Векторы  и
и 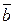 параллельны, если их соответствующие координаты пропорциональны
параллельны, если их соответствующие координаты пропорциональны
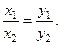
Определение 5. Векторным произведением вектора  на вектор
на вектор  называется вектор c, который:
называется вектор c, который:
1. перпендикулярен векторам  и
и  ;
;
2. имеет длину  ,
,  - угол между векторами
- угол между векторами  и
и  ;
;
3. с конца вектора  кратчайший поворот от вектора
кратчайший поворот от вектора  к вектору
к вектору  виден совершающимся против часовой стрелки.
виден совершающимся против часовой стрелки.
Обозначается 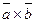
Геометрический смысл векторного произведения: в результате векторного произведения получается вектор, длина которого численно равна площади параллелограмма, построенного на векторах  и
и  как на сторонах.
как на сторонах.
Свойства векторного произведения:
1.  ;
;
2.  ;
;
3.  ;
;
4. 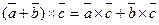 .
.
Если  , тогда
, тогда  .
.