 |
|
Спектральное представление непериодических функций — интегральное преобразование Фурье.
Реферат
По дисциплине:
«ОиРРИ»
Тема :
Интеграл Фурье, спектр (спектральная плотность) непериодической функции
Выполнил
Скобелев В.В.
Группы ИТА-4-08
Факультет: Информационные технологии
Москва 2012
Оглавление
Введение. 3
Интеграл Фурье. 4
Преобразование Фурье. 6
Свойства. 6
Спектральное представление непериодических функций — интегральное преобразование Фурье. 9
Представление непериодических функций времени с помощью интеграла Фурье. 9
Заключение. 11
Введение
Из теории Фурье известно, что при некотором воздействии на физические, технические и другие системы, его результат повторяет форму начального входного сигнала, отличаясь только масштабным коэффициентом. Понятно, что на такие сигналы (их называют собственными) система реагирует наиболее простым образом. Если произвольный входной сигнал есть линейная комбинация собственных сигналов, а система линейна, то реакция системы на этот произвольный сигнал есть сумма реакций на собственные сигналы. И поэтому полную информацию о системе можно получить по «кирпичикам» – откликам системы на собственные входные сигналы. Так поступают, например, в электротехнике, когда вводят частотную характеристику системы (передаточную функцию). Для наиболее простых линейных, инвариантных во времени систем (например, описываемых обыкновенными дифференциальными уравнениями с постоянными коэффициентами) в некоторых случаях собственными функциями являются гармоники вида 
. Таким образом можно получить и результат произвольного воздействия на систему, если последний будет представлен в виде линейной комбинации гармоник (в общем случае, в виде ряда Фурье или интеграла Фурье). Вот одна из причин, по которой в теории и приложениях возникает потребность применения понятия тригонометрического ряда (ряда Фурье) или интеграла Фурье.
Интеграл Фурье
Интеграл Фурье - континуальный аналог Фурье ряда. Для функции, заданной на конечном промежутке действительной оси, важное значение имеет представление ее рядом Фурье. Для функции f(x). заданной на всей оси, аналогичную роль играет разложение f в интеграл Фурье:
где
Разложение (1) можно формально строить в предположениях, обеспечивающих существование написанных интегралов. Оно справедливо, напр., для гладкой финитной функции f(x). Имеется большое число признаков, обеспечивающих равенство (1) в том или ином смысле. Подстановка (2) в (1) дает т. н. интегральную формулу Фурье
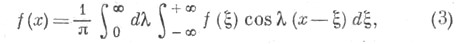
обоснование которой и приводит к упомянутым признакам. Большую пользу приносит при этом представление f(x)простым интегралом Фурье
к-рое получается из (3), если записать внешний интеграл как предел по интервалу (0, N)и поменять порядок интегрирования. В прикладных науках представление (1) часто интерпретируется как разложение по гармоникам: если
то (1) принимает вид:
и таким образом f представляется в виде суперпозиции гармоник, частоты 
которых непрерывно заполняют действительную полуось 
а амплитуда D начальная фаза 
зависят от 
Во многих случаях (в частности, для комплексно-значных функций разложение (1) удобнее представлять в экспоненциальной форме:
где
При условии, что функция f(x) суммируема: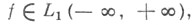 
функция 
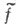ограничена, равномерно непрерывна на оси и 
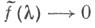при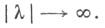 
Функция 
может оказаться несуммируемой и интеграл (4) - несуществующим. Однако равенство (4) допускает разумное истолкование, если воспользоваться методами суммирования интегралов [при этом можно рассматривать не только поточечную сходимость, но и сходимость в среднем]. Например, средние арифметические усеченных интегралов Фурье.
суммируемой функции f(x) сходятся к f(x) почти всюду и в среднем при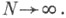 
При наличии дополнительных ограничений на функцию f(x) получаются более конкретные утверждения. Напр., если 
и имеет ограниченную вариацию в окрестности х, то
В приложениях часто используется разложение:
верное для кусочно гладкой в каждом конечном интервале абсолютно интегрируемой функции f(x), где интеграл справа понимается в смысле главного значения (6). Интеграл Фурье изучается также в предположении локальной суммируемости функции f и при тех или иных требованиях, накладывающих ограничения на поведение f в ¥. Пусть, напр., 
тогда
где предел понимается в смысле сходимости в среднем порядка 
.
ПреобразованиеФурье
Преобразование Фурье — операция, сопоставляющая функции вещественной переменной другую функцию вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие — гармонические колебания с разными частотами.
Преобразование Фурье функции 
вещественной переменной является интегральным преобразованием и задается следующей формулой:
Отметим, что разные источники могут давать определения, отличающиеся от приведенного выбором коэффициента перед интегралом, а также знака «−» в показателе экспоненты. Все свойства в этом случае будут аналогичны, хотя вид некоторых формул может измениться.
Кроме этого, существуют разнообразные обобщения этого понятия, которые будут приведены ниже.
Свойства
Хотя формула, задающая преобразование Фурье, имеет ясный смысл только для функций класса 
, преобразование Фурье может быть определено и для более широкого класса функций, и даже обобщённых функций. Это возможно благодаря ряду свойств преобразования Фурье:
· Преобразование Фурье является линейным оператором:
· Справедливо равенство Парсеваля: если 
, то преобразование Фурье сохраняет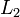 
-норму:
Это свойство позволяет по непрерывности распространить определение преобразования Фурье на всё пространство 
. Равенство Парсеваля будет при этом справедливо для всех 
.
· Формула обращения:
справедлива, если интеграл в правой части имеет смысл. В частности, это верно, если функция является достаточно гладкой. Если , то формула также верна, поскольку равенство Парсеваля позволяет придать интегралу в правой части смысл с помощью предельного перехода.
Эта формула объясняет физический смысл преобразования Фурье: правая часть — (бесконечная) сумма гармонических колебаний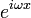 
с частотами 
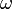, амплитудами 
и фазовыми сдвигами 
соответственно.
· Теорема о свертке: если 
, тогда
, где
Эта формула может быть распространена и на случай обобщённых функций.
· Преобразование Фурье и дифференцирование. Если 
, то
Из этой формулы легко выводится формула для 
-й производной:
Формулы верны и в случае обобщённых функций.
· Преобразование Фурье и сдвиг.
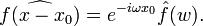
Эта и предыдущая формула являются частными случаями теоремы о свёртке, так как сдвиг по аргументу — это свёртка со сдвинутой дельта-функцией 
, а дифференцирование — свёртка с производной дельта-функции.
· Преобразование Фурье и растяжение.
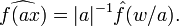
Преобразование Фурье обобщённых функций. Преобразование Фурье можно определить для широкого класса обобщённых функций. Определим вначале пространство гладких быстро убывающих функций (пространство Шварца):
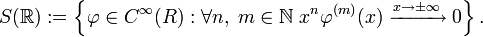
Ключевым свойством этого пространства является то, что это инвариантное подпространство по отношению к преобразованию Фурье.
Теперь определим его двойственное пространство 
. Это некоторое подпространство в пространстве всех обобщённых функций — так называемые обобщённые функции медленного роста. Теперь для функции 
её преобразованием Фурье называется обобщённая функция 
, действующая на основные функции по правилу 
Спектральное представление непериодических функций — интегральное преобразование Фурье.