 |
|
Выпуклость и вогнутость функции. Точки перегиба
Определение: Функция 
называется выпуклой вверх (выпуклой вниз) на интервале 
, если график этой функции при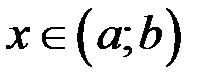 
расположен ниже (соответственно, выше) касательной, проведенной в любой его точке (рис. 2).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
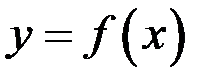
Рис. 2
Теорема 12 (достаточное условие выпуклости вверх (вниз)). Пусть функция имеет производную второго порядка на интервале . Тогда, если 
(соответственно, 
) на этом интервале, то функция выпукла вверх (соответственно, выпукла вниз) на нем.
Определение: Пусть функция дифференцируема в некоторой окрестности точки 
. Тогда если при переходе через точку функция меняет направление выпуклости, то эта точка называется точкой перегиба функции . Точка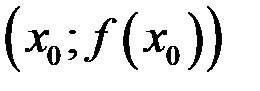 
при этом называется точкой перегиба графика функции .
Теорема 13 (необходимое условие точки перегиба). Если – точка перегиба функции , то в этой точке производная второго порядка функции либо равна нулю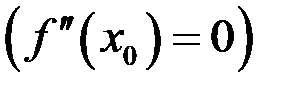 
, либо не существует.
Определение: Точки, в которых вторая производная функции равна нулю или не существует, называются критическими точками второго рода.
Теорема 14 (первое достаточное условие точки перегиба). Пусть функция непрерывна в точке и имеет производную второго порядка в некоторой окрестности этой точки (кроме, может быть, самой точки ). Тогда если при переходе через точку вторая производная меняет знак, то – точка перегиба.
Теорема 15 (второе достаточное условие точки перегиба). Пусть в точке функция имеет производные до третьего порядка включительно. Тогда если 
, а 
, то – точка перегиба этой функции.
Асимптоты
Асимптоты бывают трех видов: вертикальные, наклонные и горизонтальные.
Определение: Прямая 
называется вертикальной асимптотой графика функции , если хотя бы один из односторонних пределов 
и 
равен бесконечности.
Определение: Прямая 
называется наклонной асимптотой графика функции при 
(при 
), если 
(соответственно, 
).
Теорема 16. Прямая является наклонной асимптотой графика функции при (при ) тогда и только тогда, когда существуют конечные пределы:
и 
(соответственно,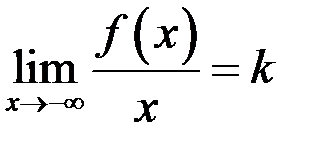 
и 
).
Определение: Наклонная асимптота , у которой 
, называется горизонтальной асимптотой.
Теорема 17. Прямая 
является горизонтальной асимптотой графика функции при (при ) тогда и только тогда, когда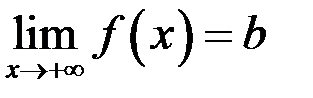 
(соответственно, 
).
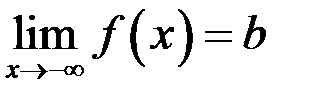Задача 6. Исследовать функцию 
и построить ее график.
Решение: Пользуясь схемой для исследования функции, получим:
Область определения 
функции – вся числовая ось, за исключением точек 
и 
, то есть:
.
Функция непериодическая. Исследуем ее на четность и нечетность:
.
Следовательно, данная функция нечетная и ее график симметричен относительно начала координат. Поэтому далее исследуем функцию только при 
.
Найдем точки пересечения графика с осями координат:
1. С осью 
график пересекается при 
, откуда 
, то есть 
– точка пересечения с осью .
2. С осью 
график пересекается, если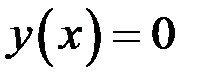 
, то есть 
, откуда .
Таким образом, – единственная точка пересечения графика функции с осями координат.
Найдем интервалы знакопостоянства функции:
,
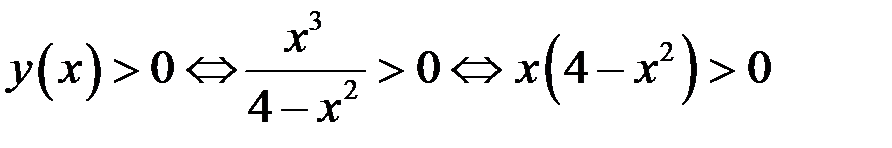и так как мы рассматриваем только случай , то получаем 
.
Аналогично 
при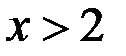 
.
Далее, 
, 
, то есть прямая 
– вертикальная асимптота.
Найдем наклонные асимптоты:
,
,
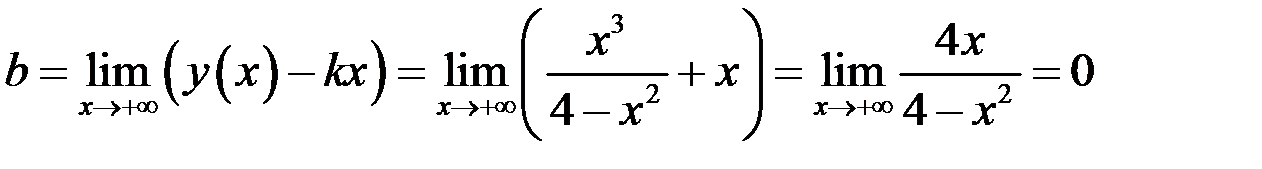то есть прямая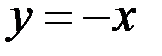 
– наклонная асимптота при 
(то же и при 
). Горизонтальных асимптот график не имеет.
Найдем интервалы монотонности и экстремумы функции, исследуя производную первого порядка:
.
Отсюда видно (рис. 3), что при 
функция имеет максимум в точке 
(причем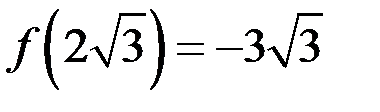 
), возрастает на 
и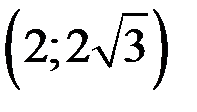 
и убывает на 
.
|
|
|
|
|
|
|
|
Рис. 3
Чтобы определить интервалы выпуклости и точки перегиба, вычислим вторую производную:
.
Следовательно, при функция выпукла вверх, то есть 
, на 
и выпукла вниз, то есть 
, на 
, 
– точка перегиба.
Учитывая полученную информацию, строим график функции при , а затем симметрично отражаем его относительно начала координат (рис. 4).
|
|
|
|
|
|
|
|
|
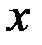
Рис. 4.
Список используемой литературы
1. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах, части 1, 2. – М.: «ОНИКС 21 век»: Мир и Образование, 2002.
2. Демидович Б.П. Сборник задач и упражнений по математическому анализу: Учеб. пособие для вузов. – М.: ООО «Издательство Астрель»: ООО «Издательство АСТ», 2004. – 558 с.
3. Кремер Н.Ш. Высшая математика для экономистов. Учебник. – М.: ЮНИТИ – ДАНА , 2007. – 479с.
Тамара Александровна Волкова,
Сергей Сергеевич Соколов
ПРОИЗВОДНАЯ
(ЗАДАНИЯ ДЛЯ ВЫПОЛНЕНИЯ