Главная | Обратная связь

ДЕЯКІ ЕКОНОМІЧНІ ЗАДАЧІ І ЇХ РОЗВ’ЯЗУВАННЯ.

Задача 1. Бюро економічного аналізу фабрики “Нова” встановило, що при виробництві х комплектів меблів щоквартальні витрати 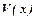виражаються формулою 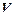( 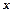) = 2050 +15 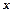(гривень), а дохід 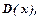одержаний від продажу 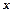комплектів меблів визначається формулою 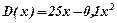(гривень).

Кожного кварталу фабрика виробляє 80 комплектів, але прагне збільшити випуск меблів до 110 одиниць. Обчислити приріст витрат, доходу та прибутку. Знайти середню величину приросту прибутку на одиницю приросту продукції.

Розв’язування.Запланований приріст продукції буде

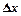= 110 - 80 = 30 (одиниць продукції ).

Приріст витрат:

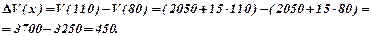
Приріст доходу:

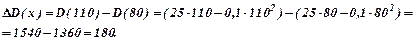Позначимо прибуток ( ).

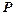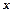Тоді .

Приріст прибутку буде:

тобто зменшиться на 270 гривень. Середня величина прибутку на одиницю приросту продукції буде .

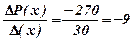Задача 2.В місті Тернополі в усіх вищих навчальних закладах навчається 35 тис. студентів. Щорічно кількість студентів збільшується на 3%. Яка кількість студентів буде в Тернополі через вісім років?

Розв’язування.Використаємо формулу зростання за складними відсотками: .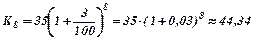

Отже, через 8 років у місті буде 44, 34 тис. студентів.

Задача 3.Вкладник надає банку 2000 гривень під складні відсотки за умови їх неперервного зростання на 12% річних. Обчислити нагромадження капіталу за 4 роки.

Розв’язування.Використаємо формулу неперервного зростання за складними відсотками: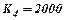

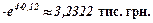
Задача 4.Сума тис.грн. вкладена під складні відсотки з розрахунку 12% річних терміном на 4 роки. Обчислити кінцеву суму, якщо відсотки нараховуються в кінці кожного місяця.

Розв’язування.Відомо, що , .

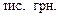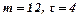Отже,

Задача 5.Закон Парето: Число у осіб, котрі мають прибуток не менш ніж х, можна визначити за формулою 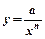(n=2, 3,……)

Даний закон достатньо точно описує розподіл великих прибутків і не справджується для низьких.

Нехай у деякому капіталістичному суспільстві розподіл прибутків серед особливо багатих осіб визначається так: 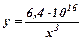, де у – число осіб, прибуток яких не менший х.

Визначити:

а)число осіб прибуток яких не менший від 100000 дол.

б) найменший прибуток серед 1000 особливо багатих осіб.

Розв’язування. Використовуючи дану формулу, знаходимо:

а) .

Отже, 64 особи мають прибуток не менший $100000.

б) з формули закону Парето одержуємо: . Якщо у=1000, то маємо: ,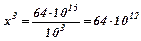

.

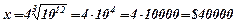Отже, найменший прибуток серед 1000 особливо багатих людей становить $40000.

Задача 6.Підприємство виготовляє 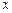виробів, роздрібна вартість кожного з них дорівнює 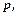причому 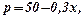а функція витрат (у гривнях). Знайти маржинальний прибуток, якщо виготовлено і продано 30 і 120 виробів.

Розв’язування.У нашому випадку функцією доходу є:

.

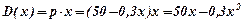Прибуток від виготовлення і продажу 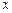виробів буде

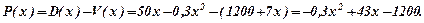Маржинальний прибуток для довільного 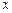дорівнює

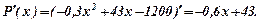
Звідси, при 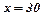і маємо:

,

.

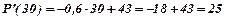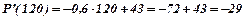Отже, при зростанні і продажу кількості виробів підприємство матиме збитки у розмірі 29 гривень за кожен виріб.

Задача 7.Знайти еластичність попиту 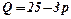стосовно ціни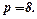

Розв’язування.Знайдемо еластичність попиту:

При 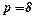маємо 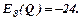Це означає, що попит є еластичним. При ціні 8 грн. підвищення її на 1% приведе до зниження попиту на 24%.

Задача 8.Заданий граничний дохід підприємства 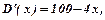де 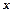- кількість виробленої продукції. Знайти функцію сумарного доходу фірми, якщо нульовий випуск продукції дає нульовий дохід.

Розв’язування. Функцію сумарного доходу можна знайти так:

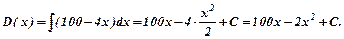
Якщо врахувати, щ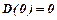о , то 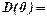С. Звідси,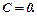

Отже, сумарний дохід підприємства

Задача 9.Маржинальний дохід фірми задається функцією

Знайти функцію доходу і визначити відношення між вартістю одиниці продукції та проданою її кількістю.

Розв’язування.Інтегруючи функцію маржинального доходу, знайдемо функцію доходу фірми:

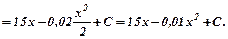
З умови, що непродаж жодної одиниці продукції дає нульовий дохід, маємо: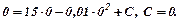

Отже, функція доходу має вигляд:

Оскільки дохід дорівнює добутку вартості кожної одиниці продукції p проданої фірмою на кількість х одиниць продукції, то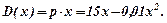

Звідси, 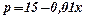.