ВКАЗІВКИ ТА ЗРАЗКИ РОЗВ’ЯЗУВАННЯ ЗАДАЧ.

⇐ ПредыдущаяСтр 2 из 2

1. Обчислити визначник: .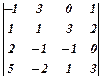

а) за допомогою елементарних перетворень:

б)розклавши за елементами рядка (або стовпця):

Розв’язування.

а) за допомогою елементарних перетворень:

(-5)

(-2)

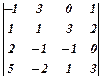
Другий рядок залишаємо без змін. Додамо до елементів першого рядка відповідні елементи другого. Додамо до елементів третього рядка відповідні елементи другого, помножені на (-2), додамо до елементів четвертого рядка відповідні елементи другого, помножені на (-5). Одержаний визначник, скориставшись теоремою розкладу, розкладемо визначник за елементами першого стовпця.

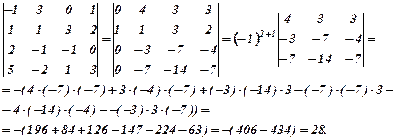
б)розклавши за елементами першого рядка , одержимо:

2. Розв’язати систему рівнянь:

а) методом Гаусса,

б)за правилом Крамера,

в)матричним методом.

Розв’язування.

´(-2)

а) заметодом Гаусса, послідовно виключаємо невідомі.

Виключимо невідому x₁ з другого і третього рівнянь. Для цього додамо перше і друге рівняння, перше рівняння помножимо на (-2) і додамо до третього, одержимо: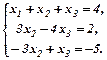

Виключимо змінну x₂ з третього рівняння. Для цього додамо друге і третє рівняння, отримуємо:

З одержаної системи, послідовно, визначаємо х₃, х₂, х₁.

Отже множина чисел є розв’язком вихідної системи лінійних рівнянь.

б) За правилом Крамера.

Знаходимо визначник системи (за правилом Саррюса):

Оскільки визначник системи відмінний від нуля, то вона завжди сумісна і має єдиний розв’язок, який знаходять за формулами Крамера:

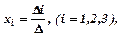
де одержуємо з визначника заміною і-го стовпця стовпцем вільних членів. Знаходимо:

Отже, ; ; ; - єдиний розв’язок системи (ЄРС).

в) Матричним методом.

Введемо позначення: .

У матричній формі систему лінійних рівнянь запишемо так .

Звідси, одержимо розв’язок: . Знайдемо обернену матрицю .

1) обчислимо визначник матриці ;

2) знайдемо алгебраїчні доповнення до елементів матриці :

;

; ; ; ; ; ; ; .

Запишемо матрицю із цих алгебраїчних доповнень:

3) Транспонуючи її, одержимо приєднану матрицю:

4) Обернена матриця має вигляд:

5) Знаходимо розв’язок системи:

Отже, x₁=1, x₂=2, x₃=1 – розв’язок заданої системи лінійних рівнянь.

3. Для виготовлення чотирьох видів продукції Р₁, Р₂, Р₃, Р₄ використовують три види сировини S₁, S₂, і S₃. Запаси сировини та норми витрат наведені в таблиці:

Вид сировини	Запаси сировини	Витрати сировини на одиницю продукції
Р₁	Р₂	Р₃	Р₄
S₁
S₂
S₃

Визначити кількість продукції Р₁, Р₂, Р₃, Р₄, яку можна виготовити, якщо сировину буде повністю вичерпано. Вказати базовий розв’язок.

Розв’язування:Якщо вважати, що х₁, х₂, х₃, х₄ – це кількість одиниць продукції Р₁, Р₂, Р₃, Р₄, то дану задачу можна записати в вигляді системи лінійних рівнянь:

що представляє собою математичну модель даної економічної задачі.

Розв’яжемо її методом Жордана-Гаусса, використовуючи таблиці:

Табл. 1. В першому рядку за ключовий елемент вибираємо 1. Цей рядок називається ключовим рядком. Переписуємо його без змін першим рядком другої таблиці. До відповідних елементів другого і третього рядків додаємо елементи першого помножені на “-2”. Результати записуємо другим і третім рядком таблиці 2.

х₁	х₂	х₃	х₄	в_і
1



-5	-2	-7	-7
-4	-3	-2	-7
		4/5	7/5	14/5
	2/5	1/5	7/5
	-7/5	-6/5	-7/5
			5/7
		-1/7
		6/7

Табл. 2. В якості ключового елемента вибираємо

“-5”. Результат ділення другого рядка на ключовий елемент, записуємо другим рядком третьої таблиці. Помноживши другий рядок таблиці 3 на “-3”, а потім на ”4”, додаючи отримані рядки відповідно до першого і третього рядків другої таблиці, отримуємо перший і третій рядки третьої таблиці, в яких відбувся процес виключення невідомої х₂.

Табл. 3. В третьому рядку ключовий елемент (-7/5) є коефіцієнтом при невідомій х₃. Тому ділимо третій рядок третьої таблиці на ключовий елемент (-7/5) і записуємо отриманий рядок третім рядком четвертої таблиці. Нам залишається виключити невідому х₃ з перших двох рядків третьої таблиці. Для цього третій рядок множимо спочатку на (-4/5) і додаємо до першого рядка третьої таблиці, а потім, множимо на (-2/5) і додаємо до другого рядка третьої таблиці. Результати дій записуємо першим і другим рядком четвертої таблиці. Таким чином ми отримали результуючу четверту таблицю, в якій кожний рядок має лише дві із чотирьох невідомих. Ця таблиця є розширеною матрицею системи рівнянь:

В останній системі рівнянь х₁, х₂, х₃ називаються базисними змінними, оскільки матриця, складена з коефіцієнтів при них є одиничною. Невідома х₄ називається вільною, тому що може приймати будь-які значення. Але в нашій задачі невідомі х_і (і=1, 2, 3, 4) виражають кількість реалізованої продукції, тому вони повинні бути невід’ємними, тобто

х_і≥ 0.

А значить Будь-якому значенню відповідає невід'ємний розв’язок, який задовольняє умові задачі. Отже, для х₄=0, х₁=2, х₂=1, х₃=1- базовий розв’язок.

4.Три фірми виробили чотири види виробів А₁, А₂, А₃, А₄. Відповідно: 13 шт.; 12 шт.; 4 шт.; 11 шт.; ІІ –13; 7; 21; 15; ІІІ – 2; 10; 12; 8. Ціна 1 шт. продукції в місті В₁ відповідно: 5 грн., 4, 3 грн., 2 грн., 1, 5 грн., в В₂ – 1; 1, 4; 3, 2; 1, 3; в В₃ – 2; 3, 6; 2, 5;. 1. Визначити дохід, який одержать фірми від продажу даної продукції в кожному з міст. ( Використати добуток матриць).

Розв’язування: Запишемо матрицю продукції , стрічки якої утворюються з чисел - кількості виробленої продукції кожною фірмою. Запишемо матрицю цін , стовпці якої утворені цінами на вироби в кожному з міст. , .

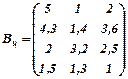Знайдемо добуток матриць А_п та В_ц –

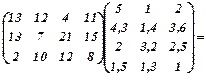
Матриця-добуток дає можливість аналізувати і порівнювати очікуваний дохід від продажу виробленої продукції. Наприклад: 141,5 –дохід першої фірми в місті В₁, 103,7 – дохід другої фірми в місті В₂, 118,7 – дохід другої фірми в місті В₃. З матриці також видно, що перша фірма одержить дохід в першому місті 141,5 грн., в другому – 56,9 грн., в третьому –90,2 грн., друга, відповідно – 939,6;103,7; 118,7; третя – 89; 64,8; 78.

5.Задані координати вершин А(2; 2), B(5; 8), C(7; 1) трикутника ABC. Знайти: а) рівняння висоти AD;б) довжину висоти AD;

в) рівняння медіани CE; г) значення кута В; д) площу трикутника АВС. Зробити малюнок.

Розв’язування.

а) Запишемо рівняння в’язки прямих, які проходять через точку А за формулою у-у_А=k(x-x_А).

У нашому випадку:y-2=k_AD(x-2). З умови перпендикулярності AD i BC одержуємо, що . Для знаходження кутового коефіцієнта k_BC запишемо рівняння сторони ВС як прямої, яка проходить через дві точки: , тобто 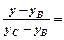; ; 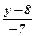= ; 2(y-8)= -7(x-5), 2y-16= -7x+35, 7x+2y-51=0 - рівняння сторони ВС.

Якщо змінну у виразити через х, то одержимо: 2y = -7x+51,

у= - . Звідси, k_BC = - , а отже, k_AD= _.

Рівняння висоти має вигляд y-2= 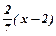, або 7y-14=2(x-2),

7y-2x-10=0.

б) Довжину висоти AD знайдемо як відстань від точки А(2; 2) до прямої ВС (7x+2y-51=0) за формулою . У нашому випадку А=7; В=2; С= -51,і тоді .

в) Медіана СЕ ділить сторону АВ трикутника АВС навпіл, тому

; .

Отже, точка Е(3,5; 5) - середина відрізка АВ. Запишемо рівняння медіани СЕ, як рівняння прямої, яка проходить через дві точки С(7; 1) i E(3,5; 5).

; ;

3,5(y-1)= -4(x-3,5); 3,5y+4x-17,5=0 або 7y-8x-35=0(CE).

г) значення кута В знаходимо за формулою , рахуючи кут від прямої з кутовим коефіцієнтом k₁ до прямої з кутовим коефіцієнтом k₂ проти годинникової стрілки . Обчислюємо кутові коефіцієнти сторін:

, .

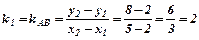. Звідси .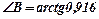

д) площу трикутника АВС знаходимо за формулою:

Довжину сторони ВС знаходимо як відстань між двома точками

;

(кв. од).

6.Скласти канонічне рівняння еліпса, який проходить через точки

М(-5; -4) i N( ). Знайти фокуси еліпса. Зробити малюнок.

Розв’язування.Нехай шукане рівняння еліпса буде .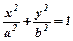

Цьому рівнянню повинні задовольняти координати точок M i N. Оскільки точка М належить еліпсу, то виконується рівність . Аналогічне рівняння отримуємо з того, що точка N належить еліпсу .

Розв’язавши систему рівнянь знайдемо величини

а і b. Отримуємо a²=50; b²=32.

Значить, рівняння еліпса має вигляд . Звідси, . Тоді координати вершин еліпса:

A₁( ; 0), A₂( ; 0), B₁(0; ), B₂(0; ).

Знайдемо величину c= .

Отже, фокуси мають координати: F₁( ; 0), F₂( ; 0).

7.Знайти границі функцій: а) ;

б) ; в) ; г) ;

д) .

Розв’язування.

а) Функція f 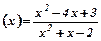в граничній точці x=1 не визначена, тому що при x=1 чисельник і знаменник дробу перетворюються в нуль, тобто маємо невизначеність виду . Розкладемо чисельник і знаменник на прості множники, знайшовши їх корені. Перетворимо дріб, розділивши чисельник і знаменник на вираз (x-1). Одержимо

.

б) У цьому випадку теж одержимо невизначеність виду . Перетворення функції f зводиться до знищення ірраціональності в чисельнику. Для цього помножимо чисельник і знаменник на спряжений вираз до чисельника, тобто на ( ), а потім скоротимо дріб на (x-3)

в) У цьому випадку має місце невизначеність виду . Розділимо чисельник і знаменник на найвищий степінь x, тобто на x³:

.

г)

Тут використано формулу: 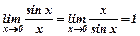- першої “визначної” границі.

д) у цьому прикладі маємо невизначеність виду . Зробимо деякі перетворення функції при знаходженні границі

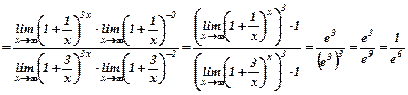. При цьому використано формулу: - другої "визначної" границі.

8.Знайти похідні функції:

а) ; б) ; в) .

Розв’язування.

а) .

Використаємо правило диференціювання для суми двох диференці-

йованих функцій, а пізніше знайдемо похідні складних функцій:

б) 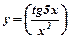. Скористаємося правилом диференціювання частки двох диференційованих функцій, а потім знаходимо похідні складних функцій:

в) .

Задану функцію прологарифмуємо, а пізніше знаходимо як похідну складної функції:

9.Підприємство за місяць виготовляє х одиниць продукції. Сумарні витрати виробництва описуються функцією , - залежність між питомою ціною і кількістю одиниць продукції х, яку можна продати по цій ціні. Розрахувати, за яких умов прибуток буде максимальним. Визначити маржинальні і сумарні витрати, прибуток при цих умовах.

Розв’язування.Прибуток 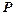визначається як різниця між доходами і сумарними витратами виробництва .

В нас дохід -

сумарні витрати -

прибуток -

Знайдемо маржинальний прибуток - .

Максимальним прибуток буде тоді, коли 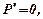оскільки

При цьому ; ; .

Отже, щоб прибуток був максимальним, треба випускати 120 од. продукції.

Маржинальні витрати -

сумарні витрати

Максимальний прибуток

10. Знайти розміри відкритого басейну з квадратним дном об’ємом 32 м³, за яких на облицювання його стін і дна пішла б найменша кількість матеріалу.

Розв’язування.Нехай дно басейну - квадрат з стороною 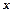, а висота басейну . Площа дна басейну: . Об’єм басейну: . Площа, яка необхідна для облицювання відкритого

басейну Оскільки то

Дослідимо функцію S(x).

Знайдемо її похідну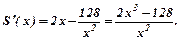

Знаходимо критичні точки: , ,

Вияснимо, як поводить себе функція при переході через критичну точку .

Обчислимо: ,

Оскільки, похідна функції змінює знак з “-” на “+” при переході через цю критичну точку, то точка є точкою мінімуму.

При ширині дна квадратної форми 4м, площа облицювання відкритого басейну буде найменша.

Знайдемо висоту басейну

Отже, розміри відкритого басейну будуть такі: дно квадратної форми має сторону квадрата 4м, висота басейну 2м.

11. При відомій функції попиту і пропозиції S=S(p)=р+1, де Qі S-кількість товару; p-ціна товару.

Знайти:

а)рівноважну ціну, тобто ціну, при якій попит і пропозиція врівноважуються;

б) еластичність попиту і пропозиції для рівноважної ціни;

в) зміну доходу при підвищенні ціни на 5% від рівноважної.

Розв’язування.

а) рівноважна ціна – ціна, при якій попит і пропозиція врівноважуються. Тому, рівноважна ціна визначається з рівняння р=3 грн.

б) знаходимо еластичність попиту і пропозиції за формулами:

В даному випадку

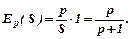
Для рівноважної ціни р=3маємо

Знайдені значення еластичності за абсолютною величиною менші за 1, тоді і попит, і пропозиція даного товару при рівноважній ціні нееластичні відносно ціни, тобто зміна ціни не призведе до різкої зміни попиту і пропозиції. Так, при підвищенні ціни на 1%, попит зменшиться на

0,75%, а пропозиція підвищиться на 0,75%.

б) при підвищенні ціни p на 5% від рівноважної, попит зменшиться на , а дохід зросте на 3,75%.

12. Дослідити та побудувати ескіз графіка функції .

Розв’язування.

1. Знаходимо область визначення функції: ]-¥; 2[È]2; +¥[.

2. Знаходимо точки перетину прямої з осями координат.

Якщо y=f(x) перетинає вісь Ох, то у=0. Якщо у=0, то х=0.

3. Досліджуємо функцію на парність.

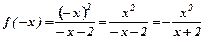. Функція є ні парна, ні непарна.

4. Досліджуємо функцію на неперервність.

В т. х=2 функція має розрив (знаменник рівний нулю, функція невизначена. ). . Це є розрив ІІ роду.

5. Знаходимо асимптоти кривої. Вертикальна асимптота х=2, тому що .

Похилу асимптоту шукаємо у вигляді y=kx+b, де ,

b= .

;

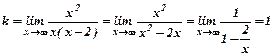Отже, рівняння похилої асимптоти має вигляд: у=х+2.

6. Досліджуємо функцію на екстремум:

Критичні точки: х=0, х=2, х=4.

Зобразимо числову пряму і проміжки монотонності:

т. х=0 – точка максимуму, f(0)=0;

т. х=4 – точка мінімуму, f(4)= .

Зробимо малюнок.

13.Мале підприємство виробляє товари А і В. Загальні щоденні витрати V (у гривнях) на виробництво х одиниць товару А та у одиниць товару В відомі: V=320 – 14х-10у+ 0, 2 х²+ 0, 1 у². 1)Визначити кількість одиниць товарів А і В, яку потрібно виробляти, щоб загальні витрати підприємства були мінімальними.

Розв’язування. Загальна функція витрат відома: V=320–14x–10y+0, 2х²+0,1 у. ² Щоб знайти кількість одиниць товарів хтовару А і у товару В, необхідно дослідити цю функцію на екстремум.

Знайдемо частинні похідні І-го порядку

Прирівнюючи їх до нуля, одержимо систему рівнянь

Знайдемо частинні похідні II порядку: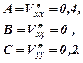

Обчислимо D=АС-В²=0, 4 0, 2-0=0, 08 > 0 і А=0, 4 > 0

Отже, функція витрат при х =35, у=50 досягає мінімуму. Це означає, що для того, щоб загальні витрати підприємства були мінімальними, необхідно виробити 35 одиниць товару А і 50 одиниць товару В.

14.Нехай виробнича функція визначається функцією Кобба-Дугласа. Щоб збільшити випуск продукції на 5%, треба збільшити фонди на 10% або чисельність робітників на 15%. В 2001 році один робітник за місяць виготовляв продукції на 2000 грн., а всього робітників було 1000. Основні фонди оцінювались в 4 млн. грн. Записати виробничу функцію, величину середньої фондовіддачі і середньої продуктивності праці, еластичність випуску по праці і по фондах.

Розв’язування. Еластичність випуску по праці , а по фондах Отже, функція Кобба-Дугласа має вигляд: ,

Підставляючи інші величини, одержимо:

, тобто

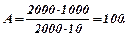
Отже, шукана виробнича функція Середня фондовіддача дорівнює а середня продуктивність , .

15.Знайти невизначені інтеграли: а) ,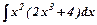

б) , в) , г) , д) , е) є) ,

ж) .

Розв’язування.

а) .

Зробимо підстановку:

Продиференціюємо: . Тому

б)

в) .

Застосовуємо метод інтегрування за частинами:

Вибираємо: u=x, dv=sin3xdx. Тоді du=dx, v= cos3x.

Тобто: .

г)

Знову інтегруємо методом інтегрування за частинами.

Підінтегральний вираз є добутком показникової функції на тригонометричну. Виберемо u= , а dv= . Тоді , Застосуємо двічі цю формулу. Два разиза uберемо . Одержуємо .

Знаходимо шуканий інтеграл:

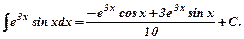
г) .

Підінтегральний раціональний дріб неправильний.

Виділяємо цілу частину:

-

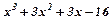
x+2+

-

7x-4

.

Використовуючи метод невизначених коефіцієнтів, розкладаємо дріб на суму простих: ; ;

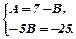В=5; А=2. Одержимо:

Тобто .

е)

Розкладемо підінтегральну функцію, яка є правильним раціональним дробом, на суму найпростіших дробів за допомогою неозначених коефіцієнтів Звідси,

Прирівнюємо коефіцієнти при однакових степенях :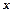

.

Тоді

є) .

Враховуємо, що cos³x=cos²xcosx, та cosxdx=dsinx. Тоді

ж) .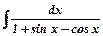

За допомогою універсальної підстановки , даний інтеграл зводимо до інтегралу від раціонального дробу. Використавши формули

; , отримаємо:

. Одержимо інтеграл від правильного дробу. Розкладемо підінтегральну функцію на прості дроби: . Звідси: . Прирівнюємо коефіцієнти при однакових степенях і складаємо систему рівнянь:

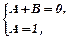
Тоді,

16.Обчислити визначений інтеграл .

Розв’язування.Зробимо підстановку .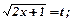

Продиференціюємо цю рівність .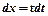

Встановимо нові межі інтегрування.

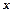
При , при . Тоді

17.Обчислити площу криволінійної трапеції, обмеженої лініями , .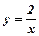

Розв’язування. Для знаходження меж інтегрування знайдемо точки перетину ліній, розв’язавши систему рівнянь .

; ; .

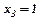Отже, площа фігури, яку треба знайти, обмежена заданими кривими, що перетинаються у точках з абсцисами , .

.

18. Обчислити об’єм тіла обертання утвореного обертанням навколо осі Ох фігури, обмеженої лініями , .

Розв’язування. Щоб знайти межі інтегрування розв’яжемо систему рівнянь

, .

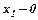Об’єм тіла обертання знаходиться за формулою

.

Отже, на основі цього маємо

(куб. од. ).

19.Швидкості зміни витрат і доходу підприємства після початку його діяльності визначались формулами:

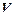і 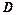вимірювали у мільйонах гривень, а - у роках. Визначити тривалість прибуткового існування підприємства і знайти загальний прибуток, що одержали за цей час.

Розв’язування. Оптимальний час для прибутку підприємства одержимо з умови

Отже, підприємство було прибутковим 1 рік. За цей час одержано прибутку:

20.Знайти загальний розв’язок (загальний інтеграл) диференціальних рівнянь та розв’язати задачу Коші для тих рівнянь, де вказані початкові умови.

а) , б) ; при , в) , г) , д) е) , є) , ж) .

Розв’язування.

а) . Це рівняння з відокремлюваними змінними. Розділимо змінні, поділивши обидві частини рівняння на . Одержимо . Проінтегруємо одержане рівняння ; , .

Сталу записали у вигляді для зручності спрощень. Далі маємо 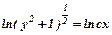; ; . Одержали загальний інтеграл рівняння.

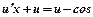
б) ; при . Дане дифрівняння однорідне, оскільки є функція від . Використаємо заміну . Тоді . Підставивши в дане рівняння, маємо ; . Розділивши змінні, одержимо . Проінтегрувавши, дістанемо ; ; або . Це загальний інтеграл даного рівняння.

Підставивши початкові умови, знайдемо : .

При такому С маємо розв’язок задачі Коші, що задовільняє даній умові: або .

в) . Розв’яжемо це рівняння методом Бернуллі. Це є лінійне неоднорідне рівняння першого порядку.

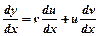Робимо заміну , (1) ; ; (2);

Прирівнюємо до нуля вираз в дужках .

Розв’язуємо диференціальне рівняння: ; ; 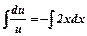, ; ; (3)

Розв’язок підставимо в рівняння (2): .

Розв’язуємо одержане рівняння: ; ⇐ Предыдущая 12