Главная | Обратная связь

Общие методические указания к выполнению контрольных работ

Согласно учебным планам и в зависимости от специальности, студент выполняет четыре или шесть контрольных работ. В таблице вариантов указаны номера задач контрольной работы. Последняя цифра зачетной книжки соответствует номеру варианта.

Контрольные работы выполняются на школьной тетради. Условия задач в контрольной работе переписываются четко без сокращений. Решения задач следует сопровождать краткими, но исчерпывающими пояснениями и, при необходимости, рисунками. Задачу желательно решать в общем виде.

 

Контрольная работа №1

 

	номер варианта
з а д а ч и

 

 

Контрольная работа №2

	номер варианта
з а д а ч и

Основные уравнения и формулы

Кинематика

Положение материальной точки в пространстве задается радиусом-вектором : ,

где – единичные векторы направлений (орты); x, y, z – координаты точки.

Скорость частицы 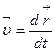. Ускорение частицы .

Формулы движения с постоянным ускорением:

; .

При криволинейном движении ускорение можно представить как сумму нормальной и тангенциальной составляющих: .

Модули этих ускорений равны: .

Угловая скорость тела 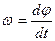. Угловое ускорение .

Кинематические уравнения равнопеременного вращения:

.

Связь между линейными и угловыми величинами:

.

План решения задач по кинематике.

1. Внимательно прочитать задачу, проанализировать условие, выяснить характер движения (равномерное, равноускоренное, прямолинейное, криволинейное). Выписать числовые значения заданных величин в системе СИ.

2. Сделать схематический чертеж, отображающий описанное в задаче движение. Изобразить на нем траекторию движения, векторы скорости, ускорения, перемещения.

3. Выбрать систему координат, при этом координатные оси направить так, чтобы проекции векторов на них выражались на них более простым образом. Отметить координаты движущегося тела в интересующие нас моменты времени, спроектировать векторы скоростей и ускорений на оси координат.

4. Составить для данного движения уравнения, отражающие математическую связь между проекциями векторов на оси координат. Составить уравнения, отражающие дополнительные условия задачи. Число уравнений должно быть равно числу неизвестных величин.

5. Решить составленную систему уравнений относительно искомых величин и поучить ответ сначала в аналитическом виде (т.е. получить расчетные формулы).

6. Подставить в расчетные формулы вместо обозначений физических величин обозначения их единиц в СИ, произвести преобразования и убедиться, получаются ли в результате единицы искомых величин.

7. Подставить в расчетные формулы числовые значения физических величин и произвести вычисления. Оценить реальность полученного результата.

 

Динамика

Уравнение движения материальной точки (второй закон Ньютона):

или .

Закон сохранения импульса: или .

Работа силы: .

Потенциальная энергия тела 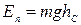. Кинетическая энергия .

Закон сохранения энергии .

Момент импульса (момент количество движения) твердого тела относительно оси вращения: .

Закон сохранения момента импульса для замкнутой системы: .

 

План решения задач по динамике.

1. Проанализировать условие задачи, понять физический процесс, рассматриваемый в ней, выяснить, какие силы действуют на интересующие нас тела.

2. Сделать схематический рисунок, изобразив на нем ки­нематические характе- ристики движения (ускорения и ско­рости), нарисовать векторы всех сил, действующих на каж­дое тело.

3. Для каждого тела в отдельности на основании второго закона Ньютона записать уравнения движения, связываю­щие проекции сил и ускорений, выбрав предварительно сис­тему отсчета. При движении тела по прямой второй закон Ньютона для тела имеет вид: ma = ΣF_i сумма, где ΣF- сумма проекций всех сил, действующих на тело, на прямую, по которой происходит движение. При этом положительное направление отсчета удобно выбирать совпадающим с на­правлением ускорения. Если направление составляющей силы совпадает с направлением ускорения, то соответству­ющая проекция силы берется со знаком плюс, в противном случае - со знаком мнус.

4. При решении задач, в которых рассматривается дина­мика равномерного движения по окружности, также целе­сообразно положительное направление координатной оси выбирать совпадающим с направлением ускорения, т.е. к центру вращения. Согласно второму закону Ньютона

где ΣF_i - сумма проекций всех сил, действующих на тело, на радиус вращения. При этом, если проекция силы направлена к центру вращения, ее нужно считать по­ложительной, если от центра - отрицательной.

5. В задачах о движении системы связанных друг с дру­гом тел одних уравнений движения оказывается недостаточ­но. В этом случае необходимо записать еще кинематические условия, выражающие собой соотношения между ускорени­ями тел системы, обусловленные связями между ними.

6. Если в задаче требуется найти не только силы и уско­рения, но также координаты (или пройденные пути) тел и их скорости, то кроме уравнений движения нужно использовать кинематические уравнения для координат и скоростей.

7. В задачах, где учитывается трение, нужно находить силу нормальной реакции опоры, определяющую силу трения. Для этого составляют уравнение на основании того, что вдоль координатной оси, перпендикулярной к направлению скорости прямолинейно движущегося тела, ускорение отсут­ствует, и поэтому сумма проекций сил на эту ось равна нулю.

8. Полученные уравнения дополнить, если необходимо, выражениями для конкретных видов сил (сила трения сколь­жения, сила трения покоя, сила упругости, сила Архимеда) и решить полученную систему уравнений в общем виде, т.е. получить расчетные формулы.

9. Убедиться, получаются ли в результате единицы иско­мых величин. Подставить в расчетные формулы числовые значения физических величин и произвести вычисления.

Колебания

Уравнение гармонических колебаний: ,

где x(t) – смещение колеблющейся величины от положения равновесия, А – амплитуда колебаний, 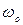- циклическая частота собственных незатухающих колебаний, - начальная фаза.

Периоды колебаний математического, пружинного и физического маятников:

, , ,

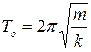где l – длина математического маятника, m- масса груза, k – коэффициент жесткости пружины, I – момент инерции маятника относительно оси колебаний, d- расстояние между точкой подвеса и центром масс маятника, g – ускорение свободного падения.

Уравнение затухающих колебаний: ,

где - коэффициент затухания, частота затухающих колебаний, - амплитуда затухающих колебаний.

Логарифмический декремент затухания: .

Период затухающих колебаний: .

 

План решения задач на колебания.

1. Задачи, решаемые с использованием уравнения гармонических колебаний.

Если известен закон, по которому изменяется х изменяется со временем, то для нахождения амплитуды колебаний, циклической частоты и начальной фазы, необходимо сопоставить данное уравнение с общим уравнением гармонических колебаний

х = Asin(ω_o+φ_ο) или х = Acos(ω_ο+φ_ο)

Затем, применяя известные соотношения, можно определить частоту и период колебаний.

Для записи законов изменения со временем скорости и ускорения тела, необходимо найти, соответственно, первую и вторую производные от координаты. Так, в случае изменения координаты по закону косинуса, получаем

y = х' = - A ω_o sin(ω_o+φ_ο) а a = х"= υ' = - Acos(ω²_ο+φ_ο).

Чтобы решить обратную задачу и написать уравнение колебаний системы исходя из условия задачи, необходимо учесть способ возбуждения колебаний, т.е. знать, где находилась система в начальный момент времени. В зависимости от этого будет определяться начальная фаза колебаний.

2. Если математический маятник, совершая колебания, движется относитель но Земли с ускорением сонаправленным или противоположно направленным ускорению свободного падения, то его период вычисляется, соответственно, по формулам

а при поднятии маятника на высоту от поверхности Земли его период увеличивается, т.к. при этом уменьшается ускорение свободного падения

где G – гравитационная постоянная, М – масса Земли, R – радиус Земли.

2. Пружинный маятник.

Если груз колеблется на нескольких пружинах, соединенных последовательно или параллельно, то в формулу для периода колебаний груза надо подставлять общий коэффициент жесткости, рассчитываемый соответственно по формулам