Молекулярно-кинетическая теория газов

Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона):

где Р –давление , V – объем, - количество вещества, m- масса газа, - молярная масса газа, R – универсальная газовая постоянная, T – температура.

Зависимость давления газа от концентрации n молекул и температуры: ,

где k – постоянная Больцмана).

Концентрация молекул газа ,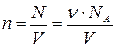

где N – число молекул в объеме газа V, N_A – постоянная Авогадро.

Скорость молекул: средняя квадратичная ,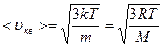

средняя арифметическая ,

наиболее вероятная .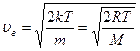

Термодинамика

Первое начало термодинамики ,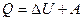

где Q – сообщенное газу; ΔU – изменение его внутренней энергии; А – работа, совершаемая газом против внешних сил.

Работа, совершаемая газом .

Внутренняя энергия идеального газа .

Молярная теплоемкость при постоянном объеме и давлении:

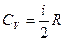
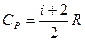Первое начало термодинамики:

при изохорном процессе ( )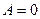

при изобарном процессе ;

при изотермическом процессе ( ) ;

при адиабатном процессе ( ) .

План решения задач.

Задачи по МКТ можно разделить на 4 типа.

1 тип задачна расчет параметров состояния газа. Для решения задачи можно рекомендовать следующую последовательность действий:

· Прочитав условие задачи, записать данные, ясно представить какие параметры газа меняются, а какие остаются постоянными.

· Записать уравнение Клапейрона-Менделеева для каждого состояния, приписывая соответствующие индексы изменяющимся параметрам.

· Записать математически все вспомогательные условия и решить полученную систему уравнений относительно неизвестной величины.

Если дана смесь газов, то уравнение Клапейрона-Менделеева записывают для каждого компонента. Давление смеси газов устанавливается законом Дальтона.

В задачах на газовые законы следует пользоваться только абсолютной температурой и сразу переводить значения температуры по шкале Цельсия в значения по шкале Кельвина.

2 тип задачна закон сохранения и превращения энергии с учетом тепловых явлений – первое начало термодинамики. Решение задач рекомендуется проводить по следующей схеме:

· Прочитать условие, записать данные.

· Установить, что является причиной изменения внутренней энергии системы – работа, совершенная системой или работа, совершенная над системой внешними силами, а также определить подводится ли к системе тепло.

3 тип задачна теплообмен между телами, составляющими замкнутую систему и составление уравнения теплового баланса. В задачах этого типа рассматриваются явления в изолированной системе, где при взаимодействиях изменяется внутренняя энергия тел без совершения работы.

· Внимательно изучить условие задачи, записать условие. Обратить внимание на то, происходит ли в процессе теплообмена изменение агрегатного состояния веществ. Четко представить в каких процессах, происходящих в системе, теплота выделяется, а в каких поглощается.

· Составить уравнения для каждого процесса, указывая, выделяется или поглощается теплота в каждом из процессов.

· Составить уравнение теплового баланса, приравняв количество теплоты, отданное телами, к количеству теплоты, полученной телами системы.

· Из уравнения теплового баланса выразить искомую величину, подставить числовые значения, провести вычисления.

При агрегатных превращениях вещества, когда заранее невозможно сказать, в каком состоянии после теплообмена окажется вещество, рекомендуется сделать предварительные числовые расчеты – найти количество теплоты Q₁, необходимое для нагревания холодного тела до температуры плавления или кипения, и количество теплоты Q₂, которое может отдать горячее тело или пар. Если Q₁< Q₂, то в состоянии теплового равновесия вещество будет находиться в двух агрегатных состояниях (пар и жидкость или жидкость и лед), в противном случае после перераспределения энергии получится одна фаза вещества. Сделав вывод о конечном результате теплообмена, можно окончательно составить уравнение теплового баланса.

4 тип задач – комбинированные задачи. Это самый сложный тип задач, т.к. в них следует применять все выше рассмотренные алгоритмы решения.

Таблица физических величин

Название константы.	Обозн.	Значение	Измерение
Гравитационная постоянная.	G	6,672∙10^-11	Н∙м²/кг²
Ускорение свободного падения	g	9,8065	м/с²
Атмосферное давление	Р_о		Па
Постоянная Авогадро	N_a	6,022045∙10²³	моль^-1
Газовая постоянная	R	8,31441	Дж/моль∙К
Постоянная Больцмана	k	1,380662∙10^-23	Дж/К
Скорость света в вакууме	c	2,99792458∙10⁸	м/с
Магнитная постоянная	μ_о	4π∙10^-7	Гн/м
Электрическая постоянная	ε_о	8,8541878∙10^-12	Ф/м
Масса покоя электрона	m_е	9,109534∙10^-³¹	кг
Масса покоя протона	m_р	1,6726485∙ 10^-27	кг
Масса покоя нейтрона	m_n	1,6749543∙10^-27	кг
Элементарный заряд	е	1,6021892∙10^-19	Кл
Отношение заряда к массе	е/m_е	1,7588047∙10¹¹	Кл/кг
Постоянная Планка	h	6,626176∙10^-34	Дж∙с
ħ	1,054887∙10^-34	Дж∙с

Задачи

1. Чему равна кинетическая энергия, которую необходимо сообщить мячу массой 1 кг, чтобы он перелетел через забор высотой h = 4 м, коснувшись его в верхней точке своей траектории? Мяч бросают с уровня h_о = 0,8 м над Землей, с расстояния S = 6,4 м от забора. Сопротивлением воздуха пренебречь.

2. Тело, брошенное вертикально вверх, упало на землю через t = 25 с. На какую высоту H поднялось тело и какова была его начальная скорость V_o?

3. Тело брошено вертикально вверх, находилось на одной и той же высоте h = 8,6 м два раза с интервалом Δt = 3 с. Пренебрегая сопротивлением воздуха, вычислить начальную скорость брошенного тела.

4. Камень, брошенный горизонтально, упал на землю через время t = 1с на расстоянии X = 5м от места бросания. Определить: - на какой высоте находился камень в начальный момент времени; - с какой скоростью он брошен; - с какой скоростью он упадет на землю; - под каким углом упал камень? Определить радиус кривизны траектории в момент падения.

5. Тело падает с высоты Н = 12,2 м. Какое расстояние пролетит тело за первые и последние 0,2 с времени своего полета?

6. Зависимость пройденного телом пути S от времени t описывается уравнением: S = A + Bt + Ct²+ Dt³, где С = 0,2 м/с² и D = 0,01м/с³. Через какое время t тело будет иметь ускорение а = 1м/с²? Найти среднее ускорение а тела за этот промежуток времени.

7. Мяч, брошенный под углом 45 с начальной скоростью Vо = 12 м/с, ударяется о вертикальную стенку. Определить время удара мяча о стенку. На какой высоте произойдет удар мяча о стенку? Какова будет скорость мяча в момент удара о стенку. Расстояние от места бросания до стенки – X = 4 м.

8. Со скалы высотой Н = 18 м в море брошен камень под углом α = 30˚ к горизонту с начальной скоростью V_o= 15 м/с. Определить время движения камня, расстояние от основания скалы до точки падения камня в воду. С какой скоростью упадет камень в воду? Какой угол составляет траектория движения камня с горизонтом в точке его падения?

9. Из одного и того же места начали равноускоренно двигаться в одном направлении две точки, причем вторая начала свое движение через 2 с после первой. Первая точка двигалась с начальной скоростью υ₁ = 1 м/с и ускорением а₁ = 2 м/с², вторая – с начальной скоростью υ₂ = 10 м/с и ускорением а₂ = 1 м/с². Через сколько времени и на каком расстоянии от исходного положения вторая точка догонит первую?

10. Найти угловое ускорение ε колеса, если известно, что через время t = 2,5 с после начала движения вектор полного ускорения точки, лежащей на ободе, составляет угол α = 60° с вектором ее линейной скорости.

11. Длина минутной стрелки часов в 2 раза больше длины секундной стрелки. Во сколько раз линейная скорость конца секундной стрелки больше линейной скорости минутной стрелки? Определить угловую скорость вращения обеих стрелок.

12. Дано угловое ускорение ε = 2 рад/с² вращающегося колеса. Определить радиус колеса, если через время t = 0,5 с после начала движения полное ускорение колеса стало а = 13,6 см/с².

13. В какой момент времени t ускорения этих точек будут одинаковы? Найти скорости и точек в этот момент времени.

14. Маховик вращается с частотой n₁ = 120 об/мин. После выключения, вращаясь равнозамедленно, до остановки он сделал N = 25 об. Определить время с момента выключения до полной остановки.

15. Определить период обращения Луны вокруг Земли, если ускорение свободного падения на полюсах Земли равно 9,83 м/с², радиус Земли 6400 км, а расстояние между центрами Земли и Луны 3,84∙10⁵ км.

16. Точка движется по окружности так, что зависимость пути от времени описывается уравнением S = A – Bt + Ct³, где В = 2м/с и С = 1м/с². Найти линейную скорость точки, ее тангенциальное, нормальное и полное ускорение через время t = 3 с, если известно, что при t = 2 c нормальное ускорение равно 0,5 м/с².

17. Точка движется по окружности радиусом R = 15см с постоянным тангенциальным ускорением а_τ. Найти нормальное ускорение а_nточки через время t = 30 с после начала движения, если известно, что к концу пятого оборота после начала движения линейная скорость точки V = 10см/с.

18. Цилиндр вращается равноускоренно. За 1 мин он получил скорость 120 рад/с. Чему равно полное ускорение точек, которые лежат на поверхности цилиндра через 1с после начала движения? Определить угол между радиусом цилиндра и полным ускорением. Радиус цилиндра 10 см. Начальная скорость равна нулю.

19. Маховик вращается равноускоренно. Найти угол α, который составляет вектор полного ускорения а любой точки маховика с радиусом в тот момент, когда маховик сделает первые 2 оборота.

20. Шкив радиусом R = 20 см приводится во вращение грузом, подвешенным на нити, постепенно сматывающейся со шкива. В начальный момент груз был неподвижен, а затем стал опускаться с ускорением а = 2 см/с². Определить угловую скорость шкива в тот момент, когда груз пройдет путь S₁ = 100 см.

21. Под действием силы F = 10 Н тело движется прямолинейно так, что зависимость пройденного телом пути S от времени t дается уравнением S = А – Вt + Ct², где С = 1 м/с². Найти массу m тела.

22. Из шланга сечением S = 6 см² направленного на стену под углом α = 60˚ к нормали ударяется струя воды и упруго отскакивает от нее без потери скорости. Скорость течения воды в струе υ = 12 м/с. Найти силу, действующую на стенку.

23. Платформа с грузом тормозится, и его скорость за время t =3,5 с равномерно уменьшается от 45 км/ч до 30 км/ч. Определить предельный коэффициент трения между платформой и грузом, чтобы при торможении груз начал скользить по платформе.

24. На горизонтальной поверхности тележки, масса которой М = 6 кг, лежит брусок массой m = 2 кг. Коэффициент трения между бруском и тележкой μ = 0,3. Чему равна минимальная сила F, с которой нужно тянуть тележку, чтобы брусок начал скользить по ее поверхности?

25. На автомобиль массой 1,5 т во время движения действует сила трения, равная 0,15 от действующей на него силы тяжести. Найти силу тяги, развиваемую мотором, если автомобиль движется с постоянной скоростью под гору с уклоном 1м на каждые 20 м пути.

26. Тягач тянет сани с лесом по ледяной дороге с постоянной скоростью 15 км/ч. С какой скоростью тягач мог бы тянуть такие сани при вывозке леса летом по грунтовой дороге, если мощность, развиваемая мотором, в обоих случаях одинакова? Коэффициент трения при движении по ледяной дороге 0,01, по грунтовой – 0,15.

27. Шарик массы m висит на нити, которая закреплена в точке О. С каким ускорением, и в каком направлении по вертикали следует перемещать точку подвеса О, чтобы натяжение нити было равно половине веса шарика?

28. На вершине двух наклонных плоскостей, составляющих с горизонтом углы 30° и 45°, укреплен невесомый блок. Два груза одинаковой массы m = 1 кг соединены нитью и перекинуты через блок. Найти ускорение движения грузов и силу натяжения нити. Трением грузов о плоскости и в блоке пренебречь.

29. Тело массой m, находящееся на вершине наклонной плоскости, удерживается силой трения. За какое время тело спустится с наклонной плоскости, если она станет двигаться в горизонтальном направлении с ускорением 1 м/с². Длина плоскости ℓ = 1 м, угол наклона к горизонту α = 30˚, коэффициент трения между телом и плоскостью μ = 0,6.

30. Грузы массой m₁ = 3 кг и m₂ = 5 кг подвешены с помощью системы блоков, как показано на рисунке. Нить считать невесомой и нерастяжимой, массой блоков пренебречь, трение в блоках не учитывать. Определить ускорение первого груза.

31. Диск вращается в горизонтальной плоскости с угловой скоростью 3 рад/с. На расстоянии 30 см от оси вращения на диске лежит небольшое тело. При каком минимальном значении коэффициента трения тело еще не будет сброшено с диска?

32. Платформа с грузом вращается вокруг вертикальной оси с частотой n=25 об/мин. Груз находится на расстоянии 20см от оси вращения. Каким должен быть коэффициент трения, чтобы груз не скатывался с платформы?

33. Тело массой m = 15 г движется по окружности радиусом R = 6 см. Найти тангенциальное ускорение тела, если известно, что к началу третьего оборота после начала движения его кинетическая энергия равна W_к = 0,7 Дж.

34. Велосипедист едет по арене цирка со скоростью 36 км/ч. Радиус арены 50 м. На какой угол он должен наклониться, чтобы не упасть?

35. Тяжелый шарик, подвешенный на нити длиной 1м, равномерно вращается по окружности в горизонтальной плоскости. Нить образует с вертикалью угол 30˚. Найти период обращения шарика.

36. В автобусе на динамометре висит груз массой 5 кг. Определить показание динамометра, если автобус едет со скоростью 72 км/ч по окружности радиусом 200м.

37. К потолку вагона подвесили на нити шарик массой 0,1 кг. При движении вагона по окружности со скоростью 108 км/ч нить отклонилась от вертикали на угол 30˚. Найти радиус окружности и силу натяжения нити.

38. На нити, которая может выдержать силу натяжения 40 Н, человек равномерно вращает тело массой 1 кг в вертикальной плоскости. Длина нити 1 м. Чему равна сила натяжения нити в тот момент времени, когда она образует с вертикалью угол 60˚?

39. Шарик массы 100 г, подвешенный на нити, качается в вертикальной плоскости так, что его ускорения в крайнем и нижнем положениях равны по модулю друг другу. Если угол отклонения нити в крайнем положении равен 30º, то сила натяжения нити в нижнем положении равна?

40. На горизонтальном диске укреплен отвес (шарик на нити), который при вращении диска вокруг вертикальной оси устанавливается под углом 45º к вертикали. Расстояние от точки подвеса до оси вращения d = 50 см, длина нити l = 56 см. Определить скорость шарика.

41. Снаряд, летящий со скоростью 30 м/с, разорвался на два осколка. Больший осколок, масса которого составляла 0,6 массы всего снаряда продолжал двигаться в прежнем направлении, но с увеличенной скоростью 45 м/с. Найти скорость меньшего осколка.

42. Мяч, летящий со скоростью v₁=15 м/с, отбрасывается ударом ракетки в противоположном направлении со скоростью v₂=20 м/с. Найти изменение импульса мяча, если известно, что изменение его кинетической энергии равно 8,75 Дж.

43. Тело массой m₁=2 кг движется навстречу второму телу массой m₂= 1,5 кг и неупруго соударяется с ним. Скорости тел непосредственно перед ударом были v₁= 1 м/с и v₂= 2 м/с. Сколько времени будут двигаться эти тела после удара, если коэффициент трения равен 0,05?

44. Тело массой m₁= 2 кг движется со скоростью v₁= 3 м/с и нагоняет тело массой m₂= 8 кг, движущееся со скоростью v₂= 1 м/с. Считая удар центральным, найти скорости тел после удара, если удар упругий.

45. Два шара с массами m₁= 0,2 кг и m₂= 0,1 кг подвешены на нитях одинаковой длины так, что они соприкасаются. Первый шар отклоняют на высоту 4,5 см и отпускают. На какую высоту поднимутся шары после удара, если удар упругий?

46. Два шарика, массы которых m₁ = 200 г и m₂ = 300 г, подвешены на одинаковых нитях длиной l = 50 см. Шарики соприкасаются. Первый шарик отклонили от положения равновесия на угол 90º и отпустили. Найти высоту на которую поднимутся шарики после абсолютно неупругого удара?

47. Тело массой m₁ движется со скоростью v₁=3 м/с и нагоняет тело массой m₂, движущееся со скоростью v₂=1 м/с. Удар считать центральным. Каково должно быть соотношение между массами тел, чтобы при упругом ударе первое тело остановилось?

48. Граната, летевшая горизонтально со скоростью 150 м/с, разорвалась на два равных осколка, которые разлетаются после взрыва под прямым углом. Один из осколков после взрыва полетел под углом α = 30º к первоначальному направлению движения гранаты. Найти скорость этого осколка.

49. Клин массы М = 2 кг находится на идеально гладкой горизонтальной плоскости. На клине лежит брусок массы m = 0,5 кг, который под действием силы тяжести может скользить по клину без трения. Наклонная плоскость клина имеет плавный переход к горизонтальной плоскости. В начальный момент система покоилась. Найти скорость клина в тот момент, когда брусок с высоты h = 1 м соскользнет на плоскость.

50. При ударе вертикально падающего шарика о металлическую горизонтальную поверхность он теряет 50% своей механической энергии. Шарик бросили на поверхность без начальной скорости с высоты h = 3,2 м. После какого по счету отскока он отскочит от нее со скоростью 1 м/с?

51. Однородный стержень массой 0,5 кг и длиной 1 м вращается в горизонтальной плоскости вокруг вертикальной оси, проходящей через середину стержня. С каким угловым ускорением вращается стержень, если на него действует момент сил М = 98,1 Н∙м.

52. Алюминиевый шар, радиусом 20 см, вращается с частотой n =5 об/с вокруг оси, проходящей через его центр. Какую работу надо совершить, чтобы увеличить угловую скорость вращения шара вдвое?

53. Маховик вращается с частотой n = 25 об/с. Его кинетическая энергия 7,85 кДж. За какое время t момент сил 50 Н∙м, приложенный к маховику, увеличит угловую скорость маховика вдвое?

54. Горизонтальная платформа массой M = 100 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой n₁= 10 об/мин. Человек массой m = 60 кг стоит при этом на краю платформы. С какой частотой n₂ начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу однородным диском, а человека – точечной массой.

55. Тонкий стержень массой m и длиной l вращается с угловой скоростью 10 с^-1 в горизонтальной плоскости вокруг вертикальной оси, проходящей через середину стержня. Продолжая вращаться в той же плоскости, стержень перемещают так, что ось вращения начинает проходить через конец стержня. Найти угловую скорость во втором случае.

56. К катящемуся по горизонтальной поверхности шару массой 1 кг приложили силу 1 Н и остановили его. Путь торможения составил 1 м. Определить скорость шара до начала торможения.

57. Платформа начинает вращаться с постоянным угловым ускорением = 0,5 рад/с и через время t₁= 15 с приобретает момент импульса L = 73,5 кг^.м²/с. Найти кинетическую энергию платформы через время t₂= 20 с после начала движения.

58. Шар и сплошной цилиндр, изготовленные из одного и того же материала, одинаковой массы катятся без скольжения с одинаковой скоростью. Определить, во сколько раз кинетическая энергия шара меньше кинетической энергии сплошного цилиндра.

59. Два одинаковых куска пластилина скользили друг навстречу другу по льду с одинаковыми кинетическими энергиями 350 Дж каждый и одновременно ударились в противоположные концы тонкого стержня, лежавшего на льду перпендикулярно направлению скоростей кусков пластилина. Масса стержня равна массе одного куска пластилина. В момент удара куски прилипли к стержню. Каково изменение полной механической энергии системы в момент удара?

60. В край однородного диска с массой M = 40 г, который может вращаться без трения вокруг закрепленной вертикальной оси симметрии, врезается летевшая горизонтально по касательной к диску пуля массой m = 20 г и застревает в нем. С какой скоростью летела пуля, если первоначально диск был неподвижен, а после удара кинетическая энергия всей системы стала равной 8 Дж?

61. В баллоне находилась масса m₁= 10 кг газа при давлении р₁= 10 МПа. Какую массу 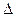m газа взяли из баллона, если давление стало равным р₂= 2,5 МПа? Температуру газа считать постоянной.

62. В закрытом сосуде объемом V = 1 м³ находится масса m₁= 1,6 кг кислорода и масса m₂= 0,9 кг воды. Найти давление р в сосуде при температуре t = 500^оС, зная, что при этой температуре вся вода превращается в пар.

63. В сосуде находится масса m₁= 14 г азота и масса m₂= 9 г водорода при температуре t = 10^оС и давлении р = 1 МПа. Найти молярную массу смеси и объем сосуда.

64. В воздухе содержится 23,6% кислорода и 76,4% азота (по массе) при давлении р = 100 кПа и температуре t = 13 ^оС. Найти плотность воздуха и парциальные давления кислорода и азота.

65. В сосуде находится масса m₁=10 г углекислого газа и масса m₂= 15 г азота. Найти плотность смеси при температуре t = 27 ^оС и давлении р = 150 кПа.

66. В сосуде объемом V = 4 л находится масса m = 1 г водорода. Какое число молекул n содержит единица объема сосуда?

67. Какое число молекул N находится в комнате объемом V = 80 м³ при температуре t = 17˚С и давлении р = 100 кПа?

68. Какое число молекул n содержит единица объема сосуда при температуре t = 10^оС и давлении р = 1,33^.10^-9 Па?

69. Воздушный пузырек на дне озера глубиной 16 м имеет объем 1,1 см³. Температура на дне равна 5˚С, а на поверхности – 16˚С. Определить объем пузырька в тот момент, когда он достигнет поверхности воды.

70. Самое низкое давление, получаемое с помощью самой совершенной вакуумной техники, приблизительно равно 10^-12 Н/м². Сколько молекул содержится при таком давлении в 1 см³ при температуре 0^оС?

71. Кислород массой m = 2 кг увеличил свой объем в n = 5 раз один раз изотермически, другой – адиабатно. Найти суммарное изменение энтропии в этих двух процессах.

72. Водород массой m = 100 г был изобарно нагрет так, что объем его увеличился в n = 3 раза, затем водород был изохорно охлажден так, что давление его уменьшилось в n = 3 раза. Найти изменение энтропии в ходе указанных процессов.

73. Три моля азота сначала изобарически нагревают в 2 раза, а затем изотермически сжимают в 3 раза. Найти изменение энтропии в этих двух процессах.

74. Два моля идеального газа сначала изохорически нагревают в е² раз (е – основание натурального логарифма), а затем адиабатически охлаждают до первоначальной температуры. Суммарное изменение энтропии в этих двух процессах ΔS = 83,1 Дж/К. Найти число степеней свободы молекул такого газа.

75. Два моля идеального газа нагревают изохорически. Определите число степеней свободы молекул такого газа, если его температура возрастает при этом в е² раз (е – основание натурального логарифма), а энтропия увеличивается при этом на величину ΔS = 49,86 Дж/К.

76. Энтропия некоторой термодинамической системы изменяется при изохорном процессе по закону 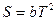, где b = 10^-5 Дж/К³. Определите изменение внутренней энергии этой системы при нагревании от температуры Т₁ = 100 К до Т₂ = 300 К.

77. В ходе некоторого процесса энтропия термодинамической системы изменяется пропорционально ее температуре Т, как показано на рисунке. Определите температуру системы, при которой ее теплоемкость станет равна 10 Дж/К?

78. Теплоемкость некоторой термодинамической системы изменяется с ростом температуры по закону 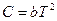, где b = 10^-5 Дж/К³. Определите изменение энтропии этой системы при ее нагревании от температуры Т₁ = 100 К до Т₂ = 300 К.

79. Внутренняя энергия некоторой термодинамической системы зависит от температуры по закону 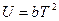. Определите величину постоянной b, если при изохорном охлаждении этой системы на ΔТ = 100 К ее энтропия уменьшается на величину ΔS = 100 Дж/К.

80. Энтропия некоторой термодинамической системы изменяется с температурой по закону 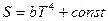, где b = 10^-5 Дж/К⁵. Определите теплоемкость этой системы при температуре Т = 300 К.

81. Два моля идеального газа совершают процесс, при котором его объем изменяется с ростом температуры по закону , где b = const. Определите молярную теплоемкость такого процесс, если молярная теплоемкость газа при постоянном объеме равна С_v = 10 Дж/К.

82. Один моль двухатомного идеального газа совершает процесс, протекающий по закону V∙Т = const, где V и Т – соответственно объем и температура газа. Найти отношение молярной теплоемкости такого процесса к универсальной газовой постоянной С/R?

83. Два моля одноатомного идеального газа расширяются так, что молярная теплоемкость газа в процессе расширения постоянна и равна С = 3R, где R – универсальная газовая постоянная. Какую работу совершит газ при изменении его температуры от Т₁ = 100 К до Т₂ = 300 К?

84. В сосуде под поршнем находится газ при нормальных условиях. Расстояние между дном сосуда и дном поршня равно 25 см. Когда на поршень положили груз массой 20 кг, поршень опустился на 13,4 см. Считая сжатие адиабатическим, найти для данного газа отношение С_р/С_v. Площадь поперечного сечения поршня равна 10 см², массой поршня пренебречь.

85. Газ расширяется адиабатически так, что его давление падает от 200 до 100 кПа. Затем он нагревается при постоянном объеме до первоначальной температуры, причем его давление возрастает до 122 кПа. Определить отношение С_р/С_v для этого газа.

86. Два моля азота совершают процесс, при котором работа зависит от температуры по закону А = RТ, где R – универсальная газовая постоянная. Найти величину молярной теплоемкости газа в этом процессе.

87. Термодинамическая система совершает циклический процесс с к.п.д. η = 75%. В состояниях 1, 2 и 3 она имеет, соответственно, температуры Т₁ = 300 К, Т₂ = 500 К и Т₃ = 400 К. Процессы 1-2 и 1-3 имеют постоянные молярные теплоемкости С₁ и С₂ соответственно, процесс 2-3 – адиабата. Вычислить отношение теплоемкостей С₁/С₂.

88. Термодинамическая система совершает циклический процесс. Молярные теплоемкости процессов 1-2 и 3-4 равны соответственно С₁ = 2 Дж/К и С₂ = 7 Дж/К. Процессы 2-3 и 4-1 адиабатические. Найти к.п.д. цикла, если известно, что изменение абсолютной температуры системы в ходе процесса 1-2 больше изменения температуры при процессе 4-3 в четыре раза.

89. Термодинамическая система совершает циклический процесс, состоящий из трех процессов 1-2, 2-3 и 3-1 с постоянными теплоемкостями С₁₂ = 2 Дж/К, С₂₃ = 6 Дж/К и С₃₁ = 8 Дж/К соответственно. Найти температуру системы в состоянии 3, если в состояниях 1 и 2 ее температура равна Т₁ = 300 К и Т₂ = 250 К соответственно, а к.п.д. всего цикла равен 20%.

90. Процесс 1-2 с постоянной теплоемкостью С₁₂ = 4 кДж/К повышает температуру газа в два раза, а процесс 2-3 с теплоемкостью С₂₃ =3 кДж/К повышает температуру газа еще в три раза. Найти к.п.д. этого цикла, если теплоемкость процесса 3-1 равна С₃₁ = 2 кДж/К.

91. Найти к.п.д. циклического процесса, изображенного на Т-S диаграмме.

92. Один моль идеального трехатомного газа совершает циклический процесс, изображенный на Р-V диаграмме, где Р₂ = 2Р₁, а V₂ = 3V₁. Найти к.п.д. этого цикла.

93. Один моль идеального двухатомного газа совершает циклический процесс, изображенный на Р-V диаграмме, где Р₂ = 2Р₁, а V₂ = 2V₁. Найти к.п.д. этого цикла.

94. Один моль идеального одноатомного газа совершает циклический процесс, изображенный на Р-V диаграмме, где Р₂ = 3Р₁, а V₂ = 2V₁. Найти к.п.д. этого цикла.

95. Идеальный одноатомный газ совершает циклический процесс, состоящий из изобары, изохоры и изотермы. Найти к.п.д. этого цикла, если и температура, и объем газа изменяются в пределах цикла в 2 раза.

96. Один моль идеального трехатомного газа совершает циклический процесс, изображенный на Р-V диаграмме, где Р₂ = 3Р₁, а V₂ = 5V₁. Найти к.п.д. этого цикла.

97. Два моля идеального одноатомного газа совершают замкнутый цикл, изображенный на рисунке. Известно, что температура Т₁ = 280 К, Р₂/Р₁ = 5, Т₄/Т₁ = 2. Определите к.п.д. этого цикла.

98. Идеальный газ совершает цикл Карно, причем за все время цикла наибольшая средняя скорость молекул газа в два раза больше наименьшей средней скорости молекул. Найти к.п.д. цикла.

99. Идеальный газ совершает цикл Карно. При этом максимальное значение средней скорости молекул газа за все время цикла оказывается в два раза больше минимального значения наиболее вероятной скорости молекул газа за время цикла. Найти к.п.д. цикла.

100. Идеальный газ совершает цикл Карно, причем за все время цикла максимальная наиболее вероятная скорость молекул газа оказывается равной минимальной средней квадратичной скорости молекул газа за время этого цикла. Найти к.п.д. цикла.

101. Идеальный газ находится в сосуде под поршнем. Первоначальная температура газа равна Т₁ = 300 К, а частота соударений молекул о стенки сосуда n₁ = 10¹⁰м^-2с^-1. Температуру газа в сосуде изменяют , но давление газа при этом остается неизменным. Найти температуру газа Т₂, при которой частота соударений молекул о стенку станет равной n₂ = 2∙10¹⁰м^-2с^-1.

102. При температуре 0˚С и некотором давлении средняя длина свободного пробега молекул кислорода равна 95 нм. Чему равно среднее число столкновений в 1 с молекул кислорода, если сосуд откачать до 0,01 первоначального давления? Температура остается неизменной.

103. При некоторых условиях средняя длина свободного пробега молекул газа равна 160 нм и средняя арифметическая скорость его молекул равна 1,95 км/с. Чему будет равно среднее число столкновений в 1 с молекул этого газа, если при той же температуре давление газа уменьшить в 1,27 раза?

104. Найти среднее число столкновений в 1 с молекул некоторого газа, если средняя длина свободного пробега при этих условиях равна 5 мкм, а средняя квадратичная скорость его молекул равна 500 м/с.

105. В сосуде под поршнем находился идеальный газ, молекулы которого соударялись со стенками сосуда с частотой n₁ = 1,2∙10¹⁰м^-2с^-1. Затем поршень медленно сжали, в результате чего объем газа уменьшился в два раза, а давление возросло в 8 раз. Чему равна частота n₂ соударений молекул этого газа со стенками после сжатия?

106. Молекулы идеального газа, находящегося в закрытом сосуде под давлением Р = 4∙10⁴ Па, соударяются со стенками сосуда с частотой n = 10²⁷м^-2с^-1. Известно, что k∙m = π^-1∙10^-48 Дж∙кг/К, где k – постоянная Больцмана, m – масса одной молекулы. Какова температура газа?

107. Средняя скорость молекул газа в закрытой трехлитровой банке равна 2000 м/с. Найти число молекул этого газа, если за одну секунду с 1 см² поверхности стенки внутри банки сталкивается 10²¹ молекул.

108. В закрытой литровой банке имеется N = 6∙10²⁰ одинаковых молекул одноатомного газа. Найти массу каждой молекулы, если известно, что средняя энергия одной молекулы этого газа <E> = 1,57∙10^-20 Дж, а частота соударений молекул со стенками банки равна n = 10²⁶м^-2с^-1.

109. При температуре идеального газа Т₁ = 300 К средняя длина свободного пробега его молекул была равна λ₁ = 6∙10^{-7 м. Затем температуру газа изменяют при постоянном давлении. Считая, что эффективный диаметр молекул при этом не меняется. Найти температуру Т}₂ при которой средняя длина свободного пробега молекул станет равной λ₂ = 4,5∙10^{-7 м.}

110. После того, как идеальный газ нагрели, средняя длина свободного пробега молекул этого газа возросла в 1,8 раз, а частота соударений его молекул о стенки сосуда уменьшилась в 1,2 раза. Во сколько раз возросла температура газа при нагревании? Эффективный диаметр молекул газа при этом практически не меняется, а давление и объем газа изменяются.

111. Однородный шарик подвешен на нити, длина которой равна радиусу шарика. Во сколько раз период малых колебаний этого маятника больше периода малых колебаний математического маятника с таким же расстоянием от центра масс до точки подвеса?

112. Найти период колебаний однородного стержня длиной l = 0,5 м, совершающего колебания в вертикальной плоскости около горизонтальной оси, проходящей через точку на расстоянии 10 см от его верхнего конца.

113. На концах вертикального стержня укреплены два груза. Центр масс грузов находится ниже середины стержня на расстоянии d = 5 см. Найти длину стержня, если известно, что период малых колебаний стержня с грузами вокруг горизонтальной оси, проходящей через его середину, Т = 2 с. Массой стержня пренебречь по сравнению с массой грузов.

114. Уравнение движения точки дано в виде x = sin 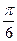t. Найти моменты времени, в которые достигаются максимальная скорость и максимальное ускорение.

115. Математический маятник колеблется в некоторой вязкой жидкости, причем амплитуда колебаний уменьшается за период в exp(2 ) раз (где ln e = 1). Во сколько раз период таких колебаний будет больше периода незатухающих колебаний этого же математического маятника при отсутствии жидкости?

116. Найти логарифмический декремент затухания математического маятника, если за время t = 1 мин амплитуда колебаний уменьшилась в 2 раза. Длина маятника 1 м.

117. Начальная фаза гармонического колебания равна нулю. При смещении точки от положения равновесия x₁= 2,4 см скорость точки v₁= 3 см/с, а при смещении x₂= 2,8 см ее скорость v₂= 2 см/с. Найти амплитуду и период этого колебания.

118. Амплитуда затухающих колебаний математического маятника за время t₁= 1 мин уменьшилась вдвое. Во сколько раз уменьшится амплитуда за время t₂= 3 мин?

119. К пружине подвешена чашка весов с гирями. При этом период вертикальных колебаний Т₁= 0,5 с. После того как на чашку весов положили еще добавочные гири, период вертикальных колебаний стал равным Т₂=0,6 с. На сколько удлинилась пружина от прибавления этого добавочного груза?

120. Грузик на пружинке жесткости k колеблется в некоторой жидкости, причем частота его колебаний 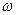в два раза меньше собственной частоты незатухающих колебаний грузика на той же пружинке. Коэффициент жесткости пружинки увеличили в 7 раз. Во сколько раз надо увеличить коэффициент вязкого трения жидкости, чтобы период колебаний грузика не изменился?