Побудова лінійної моделі парної регресії

Методичні вказівки до виконання розрахункової частини контрольної роботи

Для вирішення першого завдання бажано використовувати надбудову «Пошук рішень» Microsoft Excel для автоматизації та швидкості розрахунків.

Надбудова «Пошук рішень» Microsoft Excel використовує алгоритм нелінійної оптимізації Generalized Reduced Gradient (GRG2), розроблений Леоном Ласдоном (Leon Lasdon, University of Texas at Austin) і Аланом Уореном (Allan Waren, Cleveland State University).

«Пошук рішень» є частиною блоку завдань, який іноді називають аналіз "що - якщо". Процедура пошуку рішень дозволяє знайти оптимальне значення функції, яка записана в клітині та називається цільовою. Ця процедура працює із групою клітин, прямо або непрямо пов'язаних з формулою в цільовій клітині. Для одержання бажаного результату процедура «Пошук рішень» змінює значення в тих клітинах, які впливають на цільову функцію Щоб звузити безліч значень, які використовуються у моделі, застосовуються обмеження, які, в свою чергу, теж можуть впливати на інші значення інших клітин.

Надбудову «Пошук рішень» можна використовувати для визначення значення клітини, яка впливає та відповідає екстремуму залежної клітини (наприклад, як зміна фонду робочого часу чи продуктивність праці робітників вплине на прогнозовану суму витрат або отриманого прибутку).

Приклад застосування надбудови «Пошук рішень»:

Керівництво промислового підприємства отримало замовлення на виробництво 40 тис. виробів 1-го сорту(В₁) і 6 тис. виробів (В₂) 2-го сорту.

Продукція виробляється в двох цехах, а собівартість виготовлення в першому цеху одиниці продукції 1-го сорту становить 180 грн., одиниці 2-го сорту – 350 грн., а для другого цеху – 320 і 600 грн. відповідно. Дані щодо продуктивності праці та фондів робочого часу надані у таблиці 4:

Таблиця 4

Цех	Продуктивність праці (кількість продукції за одиницю часу – 1годину)	Фонд робочого часу, годин
В₁, тис. шт.	В₂, тис. шт.
Ц₁
Ц₂
Замовлення, тис. шт.

Складіть математичну модель завдання, яка дозволить знайти оптимальний обсяг випуску виробів, що забезпечує мінімальні витрати на виконання замовлення.

Визначте загальну собівартість виконання замовлення промисловим підприємством.

Яку саме кількість виробів кожного сорту повинні виробити працівники відповідних цехів?

Розв’язання

Вихідні величини – обсяги випуску виробів.

Так як вироби В₁ та В₂ виготовляються цехами Ц₁ та Ц₂, то треба розрізняти 4 змінні. Будемо використовувати двоіндексну форму запису х_ij – кількість виробів В_j (j=1,2), які виготовляються Ц_i (i=1,2), тобто отримуємо:

х₁₁ – кількість виробів В₁, які виготовляються Ц₁, шт.; і т.д.

Мета вирішення задачі – виконання плану з мінімальними витратами, тобто критерій ефективності є показник витрат на виконання всього замовлення. Виходячи із витрат кожного цеху, отримуємо цільову фукнцію:

L(x) = 180x₁₁ + 350x₁₂ + 320x₂₁ + 600x₂₂ →min, [грн./ шт. * тис. шт. = тис. грн.]

Можливі обсяги виробництва цехів обмежуються наступними умовами:

- загальний обсяг виробів В₁, який випущений обома цехами, становить – 40 шт. , а В₂ – 6 шт.;

- час, який витрачений на роботу складає для Ц₁ – 8 годин, а Ц₂ – 6 годин;

- обсяги виробництва не можуть бути негативними величинами.

Отже, математично обмеження щодо обсягу випуску запишемо:

х₁₁ + х₂₁ = 40 [тис. шт. = тис. шт.]

х₁₂ + х₂₂ = 6 [тис. шт. = тис. шт.]

Обмеження щодо фонду робочого часу – тут виникає проблема, тому що за умовами заадчі не заданий час, який витрачають цех на виробництво одного виробу (трудомісткість), але задана продуктивність цеху.

Т_р = 1/П_р

Отже, використовуючи таблицю, ми запишемо:

1/5 години – час, який витрачає Ц₁ на виготовлення В₁, год.;

1/3 години – час, який витрачає Ц₁ на виготовлення В₂, год.;

1/1 години – час, який витрачає Ц₂ на виготовлення В₁, год.;

1/4 години – час, який витрачає Ц₂ на виготовлення В₂, год.

Математично обмеження щодо фонду робочого часу запишемо:

х₁₁/5 + х₁₂/3 = 8 [год./тис. шт. * тис. шт. = год.]

х₂₁ + х₂₂ = 6 [год./тис. шт. * тис. шт. = год.]

Позитивність обсягів випуску запишемо:

x_ij ≥ 0 при i=1,2; j=1,2.

Таким чином, математична модель матиме вигляд:

L(x) = 180x₁₁ + 350x₁₂ + 320x₂₁ + 600x₂₂ →min, [тис. грн.]

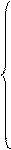х₁₁ + х₂₁ = 40 [тис. шт.]

х₁₂ + х₂₂ = 6 [тис. шт.]

х₁₁/5 + х₁₂/3 ≤ 8 [год.]

х₂₁ + х₂₂/4 ≤ 6 [год.]

x_ij ≥ 0 при i=1,2; j=1,2.

Для відповіді на наступні питання доцільно використовувати надбудову «Пошук рішень» табличного процесору MS Excel.

Отже, запускаємо MS Excel та створюємо нову робочу книгу.

Перед початком роботи зі згаданою надбудовою, потрібно створити робочий лист та ввести допоміжні дані.

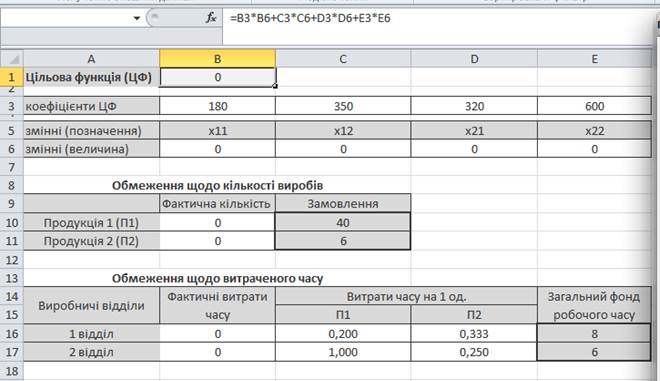На цьому етапі заповнюємо робочий лист згідно нижче наведеного прикладу:

А розроблену математичну модель з обмеженнями представимо у вигляді формул, які використовуються в MS Excel:

Далі внесемо формули та значення у відповідні клітини на робочому листі.

Після цього викликаємо надбудову «Пошук рішень» та заповнюємо її згідно нижче наведеного прикладу:

Після внесення всіх параметрів натискаємо кнопку «Найти решение».

Відкривається наступне діалогове вікно:

Обираємо зберегти найдене рішення та натискаємо кнопку ОК.

Отже, отримуємо результати:

- загальну собівартість виконання замовлення, яка становить 10750 тис. грн. (клітина B1);

- кількість виробів, які виробляються відповідними цехами:

· 1-й цех 35 тис. виробів 1-го сорту та 3 тис. виробів 2-го сорту (клітини B6 та С6 відповідно);

· 2-й цех 5 тис. виробів 1-го сорту та 3 тис. виробів 2-го сорту (клітини D6 та E6 відповідно).

Для вирішення другого завдання доцільно скористатись надбудовою «Аналіз даних» MS Excel або ж програмний комплекс Statistica.

На нижче наведеному прикладі висвітлимо основні етапи побудови лінійної, степеневої та показникової економетричних моделей та оцінимо параметри отриманих моделей, використовуючи надбудову «Аналіз даних» MS Excel.

Приклад

За даними таблиці 5 побудуйте регресійну, показникові та степеневу моделі залежності попиту на продукцію від ціни реалізації.

Таблиця 5

Вихідні дані

№ з/п	Попит на продукцію, тис. грн.	Ціна, грн.
	60,60	205,39
	40,30	206,42
	50,20	206,23
	70,40	205,40
	50,80	206,96
	60,40	206,54
	50,70	205,69
	60,90	207,84
	60,60	207,09
	80,00	209,19
	80,70	206,74
	80,00	206,84

Побудова лінійної моделі парної регресії

Припустимо, що зв'язок - лінійний. Рівняння лінійної регресії має вид:

y_x=a₀+a₁*x

Побудова рівняння лінійної регресії зводиться до оцінки її параметрів, для якого використовують надбудову MS Excel «Аналіз даних» та інструмент «Регресія».

Порядок побудови складається з наступних етапів:

1. 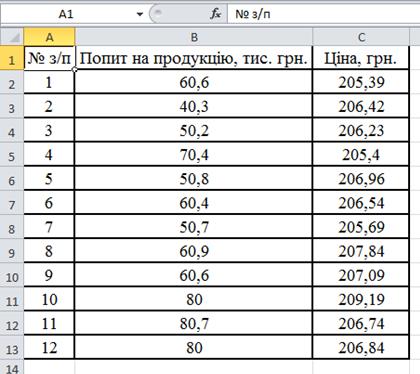На робочому аркуші сформувати таблицю, що містить вихідні дані.

2. Завантажуємо надбудову «Аналіз даних»

та обираємо інструмент «Регресія». Відкривається наступне діалогове вікно:

3. У блоці «Входные данные»:

a. В полі «Входной интервал по Y» необхідно вказати діапазон даних В2:В13.

b. В полі «Входной интервал по Х» необхідно вказати діапазон даних С2:С13.

c. В полі «Уровень надежности» вказати «95 %».

4. У блоці «Параметры вивода» необхідно вказати місце куди, будуть виведені отримані результати – визначений діапазон, новий робочий лист чи робоча книга.

5. Натиснути «Ок».

Отримуємо наступні дані:

Таким чином теоретичне рівняння лінійної регресії має вигляд:

y = - 890,817 + 4,61*х

Оскільки а₁>0, то регресія невід’ємна, тобто збільшення значення х веде до збільшення значення у.

Коефіцієнт регресії (а₁) свідчить, що при збільшенні ціни на 1 одиницю попит збільшиться на 4, 61 одиниць.

Коефіцієнт детермінації R²= 0, 1369, тобто варіація результату у на 13,7% пояснюється варіацією фактора х, на долю не врахованих факторів залишається 86,3%.

Стандартна похибка становить 12,93.

Для визначення якості обраної моделі доцільно розрахувати середню помилку апроксимації:

Тобто в середньому розрахункові значення відхиляються від фактичних на 17,20%, що вказую на невисоку якість моделі.

Оцінку значущості рівняння регресії проводимо за допомогою критерію Фішера, для чого порівнюються табличне значення F_таблвідповідного рівня значимості з фактичним F_факт:

F_факт=1,587

При α=0,05, k₁=m=1, k₂=n-m-1=10

F_табл=4,96

Оскільки F_факт<F_табл, то рівняння регресії з ймовірністю 95% визначається в цілому як статистично не значиме.

12 Следующая ⇒