Главная | Обратная связь

Вывод формулы производной сложной функции.

Определение касательной и нормали к плоской кривой. Вывод их уравнений.

 

Касательной к данной кривой в данной на ней точке M₀ называется предельное положение секущей при условии, что точка M₁, перемещаясь по этой кривой, неограниченно приближается к точке M₀.

Рассм. M₀CM₁: M₀(x₀;y₀) M₁(x₁,y₁)

tgb=M₁C/M₀C M₀C=x₁-x₀=Dx M₁C=y₁-y₀=Dy

Нормалью данной кривой в данной на ней точке называется прямая, проходящая через эту точку перпендикулярно касательной в этой точке.

 

Теорема о производной суммы двух функций.

Производная суммы двух дифференцируемых функций равна сумме производных слагаемых.

y=u+v, u=u(x), v=v(x).

u и v диф. в т. x=x₀.

DxÞDu, DvÞDy

y+Dy=u+Du+v+Dv

Dy=u+Du+v+Dv-y= u+Du+v+Dv-u-v=Du+Dv

 

Теорема о производной произведения двух функций.

Производная произведения двух дифференцируемых функций (y = uv) существует и вычисляется по формуле:

Док-во:

DxÞDu, DvÞDy

y+Dy=(u+Du)(v+Dv)=uv+Duv+uDv+DuDv

Dy= uv+Duv+uDv+DuDv-uv=Duv+uDv+DuDv

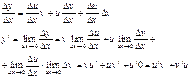
Теорема о производной частного двух функций доказывается аналогично.

Вывод формулы для производной логарифмической функции.

 

Вывод формул для производных sinx, cosx

 

y=sinx:

Dx; Dy=f(x₀+Dx)-f(x₀)

Dy=sin(x₀+Dx)-sinx₀=2sin(Dx/2)cos(x₀+Dx/2)

y=cosx:

Dx; Dy=f(x₀+Dx)-f(x₀)

Dy=cos(x₀+Dx)-cosx₀=-2sin(Dx/2)sin(x₀+Dx/2)

 

Вывод производных показательной и степенной функций.

 

Производная показательной функции:

 

Производная степенной функции:

x < 0 y = x^α z = - x , z > 0

y = (-1) ^α z ^α

y’ = (-1) ^α α z ^α-1 (-x)’ = -(- 1) ^α α (-x) ^α-1 = (- 1) ^{α +α -1+1} = α x ^{α - 1}

Вывод формулы производной сложной функции.

Если функция x=j(t) дифференцируема в точке t₀, а функция y=f(x) дифференцируема в точке x=x₀=j(t₀), то сложная функция y=f(j(t)) дифференцируема в точке t=t₀ и ее производная в этой точке находится по формуле

Док-во:

Т. к. функция y=f(x) дифференцируема в точке x=x₀, то Dy=f ‘(x₀)Dx+a(Dx)Dx.

9. y=arcsinx. Определение. Вывод производной.

arcsinx - угол, синус которого равен x.

при x = ±1 производной не существует

Свойства : Эта функция определена на отрезке -1≤ х ≤1 . её значения заполняют отрезок –π /2≤ y ≤π /2 .