 |
|
Геометрический смысл дифференциала.
Дифференциалом дифференцируемой функции называется главная, линейная относительно Dx, часть приращения функции. 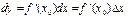
Дифференциал функции в данной точке равен приращению ординаты касательной. График
Связь дифференцируемости с существонием производной
Для того, чтобы ф-ция y=f(x) была дифференцируемой в точке x=x0, необходимо и достаточно, чтобы она имела в этой точке производную.
1.(15) Необходимость.
Дано: Dy=ADx+a(Dx)Dx, 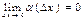
Док-ть; 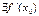 .
.
Док-во:

Достаточность.
Дано: 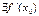 .
.
Док-ть: Dy=ADx+a(Dx)Dx, 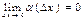
Док-во: 
∆y = ∆x·f´(∆x)+α(∆x)·∆x 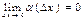
Возрастание, убывание функции. Теорема о достаточном условии монотонности функции.
Функция y=f(x) называется возрастающей [убывающей] на интервале (a;b), если из неравенства x2>x1 следует неравенство f(x2)>f(x1) [f(x2)<f(x1)] при условии, что (x1;x2)Ì(a;b).
Если функция y=f(x) дифференцируема на интервале (a;b) и f ‘(x)>0 [f ‘(x)<0] на этом интервале, то эта функция возрастает [убывает] на этом интервале.
Доказательство:
Возьмем две произвольные точки: x1,x2Î(a;b);
x0Î(a;b), x2>x1.
Рассм. отрезок [x1,x2]. На нем функция y=f(x) удовлетворяет всем условиям теоремы Лагранжа.
По теореме Лагранжа найдется xÎ(x1;x2), что выполняется равенство f(x2)-f(x1)=f ‘(x)(x2-x1).
1) f ‘(x)>0 Þ x2-x1>0 ; f ‘(x)>0 Þf(x2)-f(x1)>0
f(x2)>f(x1).
2) f ‘(x)<0
f ‘(x)<0
x2-x1>0,Þf(x2)-f(x1)<0
f(x2)<f(x1)
Определение максимума и минимума. Док-во необходимого условия экстремума.
Функция y=f(x) имеет максимум [минимум] в точке x=x0, если найдется такая окрестность этой точки, что для всех x из этой окрестности выполняется неравенство f(x0)>f(x) [f(x0)<f(x)].
Если функция y=f(x) имеет в точке x=x0 экстремум, то ее производная в этой точке равна 0 или не существует.
Дано: x=x0 -точка максимума.
Док-ть: f ‘(x0)=0.
Док-во:
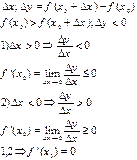
(для минимума - по аналог. док-ву)