Главная | Обратная связь

Геометрический смысл производной, касательная

Производная

 

Физический смысл производной

 

1.Ма­те­ри­аль­ная точка дви­жет­ся пря­мо­ли­ней­но по за­ко­ну (где x — рас­сто­я­ние от точки от­сче­та в мет­рах, t — время в се­кун­дах, из­ме­рен­ное с на­ча­ла дви­же­ния). Най­ди­те ее ско­рость в (м/с) в мо­мент вре­ме­ни t=3 c.

2. Ма­те­ри­аль­ная точка дви­жет­ся пря­мо­ли­ней­но по за­ко­ну , (где x — рас­сто­я­ние от точки от­сче­та в мет­рах, t — время в се­кун­дах, из­ме­рен­ное с на­ча­ла дви­же­ния). В какой мо­мент вре­ме­ни (в се­кун­дах) ее ско­рость была равна 4 м/с?

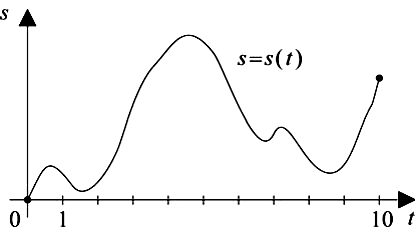
3. Материальная точка М начинает движение из точки и движется по прямой в течение 10 секунд. График показывает, как менялось расстояние от точки A до точки M с течением времени. На оси абсцисс откладывается время t в секундах, на оси ординат – расстояние s в метрах. Определите, сколько раз за время движения скорость точки M обращалась в ноль (начало и конец движения не учитывайте).

 

 

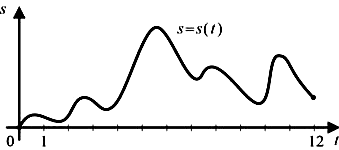4. Материальная точка M начинает движение из точки A и движется по прямой на протяжении 12 секунд. График показывает, как менялось расстояние от точки A до точки M со временем. На оси абсцисс откладывается время t в секундах, на оси ординат – расстояние s в метрах. Определите, сколько раз точка M меняла направление движения.

 

Геометрический смысл производной, касательная

 

1. Пря­мая па­рал­лель­на ка­са­тель­ной к гра­фи­ку функ­ции . Най­ди­те абс­цис­су точки ка­са­ния.

2. На ри­сун­ке изоб­ра­жен гра­фик про­из­вод­ной функ­ции f(x). Най­ди­те абс­цис­су точки, в ко­то­рой ка­са­тель­ная к гра­фи­ку па­рал­лель­на пря­мой или сов­па­да­ет с ней.

 

3. На ри­сун­ке изоб­ра­жен гра­фик функ­ции y=f(x). Пря­мая, про­хо­дя­щая через на­ча­ло ко­ор­ди­нат, ка­са­ет­ся гра­фи­ка этой функ­ции в точке с абс­цис­сой 8. Най­ди­те f'(8). (1,25)

 

4. На ри­сун­ке изоб­ра­жен гра­фик про­из­вод­ной функ­ции f(x). Най­ди­те абс­цис­су точки, в ко­то­рой ка­са­тель­ная к гра­фи­ку y=f(x) па­рал­лель­на оси абс­цисс или сов­па­да­ет с ней.

5. На рисунке изображён график функции y=f(x), определённой на интервале (1; 11). По рисунку найдите корень уравнения , принадлежащий интервалу (2; 6).

6. На ри­сун­ке изоб­ра­жен гра­фик про­из­вод­ной функ­ции f(x), опре­де­лен­ной на ин­тер­ва­ле (−10; 2). Най­ди­те ко­ли­че­ство точек, в ко­то­рых ка­са­тель­ная к гра­фи­ку функ­ции f(x) па­рал­лель­на пря­мой y = −2x−11 или сов­па­да­ет с ней.

 

На ри­сун­ке изоб­ражён гра­фик функ­ции y=f(x) и ка­са­тель­ная к нему в точке с абс­цис­сой x₀. Най­ди­те зна­че­ние про­из­вод­ной функ­ции f(x) в точке x₀.

 

7.	8.	9.
10.	11.	12.