Применение производной к исследованию функций

1.На рисунке изображён график производной функции f(x) и восемь точек на оси абсцисс: x₁, x₂,…x₈. В скольких из этих точек функция f(x) возрастает?	2. На рисунке изображён график производной функции f(x) и восемь точек на оси абсцисс: x₁, x₂,…x₈. В скольких из этих точек функция f(x) убывает?	3. На рисунке изображён график производной функции f(x) и восемь точек на оси абсцисс: x₁, x₂,…x₈. В скольких из этих точек функция f(x)возрастает?
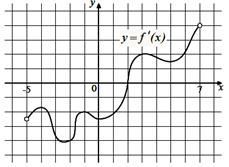
4. На рисунке изображен график производной функции f(x), определенной на интервале (−11; 11). Найдите количество точек экстремума функции f(x) на отрезке [−10; 10].	5. На рисунке изображен график функции y=f(x), определенной на интервале (−2; 12). Найдите сумму точек экстремума функции f(x).
6. На рисунке изображен график производной функции f(x), определенной на интервале (−4; 8). Найдите точку экстремума функции f(x) на отрезке [−2; 6].	7. На рисунке изображен график производной функции f(x), определенной на интервале (-18; 6). Найдите количество точек минимума функции f(x) на отрезке [-13; 1].
8. На рисунке изображён график – производной функции y=f(x),опредёленной на интервале (-2;5). По рисунку найдите точку минимума функции y=f(x).	9. На рисунке изображен график y=f'(x) – производной функции f(x), определенной на интервале (-14;9) . Найдите количество точек максимума функции f(x), принадлежащих отрезку [-12;7].
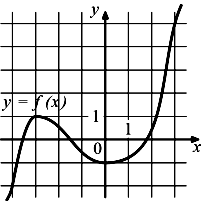
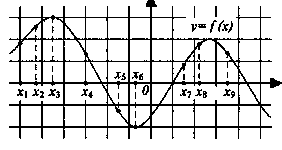
10. На рисунке изображен график y = f ′( x) – производной функции f ( x), определенной на интервале (−5; 7). В какой точке отрезка [−4; 2] функция f ( x) принимает наименьшее значение?	11. На рисунке изображен график функции y=f(x), определенной на интервале (-1;13). Найдите количество точек, в которых касательная к графику функции параллельна прямой y=-10.	12.На рисунке изображен график дифференцируемой функции y=f(x). На оси абсцисс отмечены девять точек: x₁,x₂ … x₉. Среди этих точек найдите все точки, в которых производная функции f(x) отрицательна. В ответ укажите количество найденных точек.
13. На рисунке изображен график функции y=f(x), определенной на интервале (-1;13). Найдите количество точек, в которых касательная к графику функции параллельна прямой y=20.	14. На рисунке изображён график – производной функции y=f(x),опредёленной на интервале (2;13). По рисунку найдите точку максимума функции y=f(x).
15. На рисунке изображен график y=F(x) одной из первообразных некоторой функции f(x), определенной на интервале (-8;7). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-5;5].	16. На рисунке изображен график - производной функции y=f(x), определенной на интервале (-4; 11). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.	17. На рисунке изображен график y=f(x), определенный на интервале (-3;8). Найдите количество точек, в которых производная функции f(x) равна 0.
18. На рисунке изображен график - производной функции y=f(x), определенной на интервале (-2; 9). В какой точке отрезка [2;9] функция f(x) принимает наименьшее значение.	19. На рисунке изображен график - производной функции y=f(x), определенной на интервале (-6; 5). В какой точке отрезка [-5;-1] функция f(x) принимает наименьшее значение.	20. На рисунке изображён график функции y=f(x). Найдите наибольшее значение функции f(x) на отрезке [-1; 8].
21. На рисунке изображён график функции y=f(x). Найдите наименьшее значение функции f(x) на отрезке [-7; 0].	22.На рисунке изображён график функции y=f(x). Найдите точку, в которой функция f(x) принимает наибольшее значение на отрезке [-4; 3].	23. На рисунке изображен график — производной функции, определенной на интервале (-10;2). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y=x+1 или совпадает с ней.
24. На рисунке изображен график — производной функции y=f(x), определенной на интервале (-5,7). Найдите промежутки возрастания функции f(x). В ответе укажите сумму всех целых точек, входящих в эти промежутки.	25. Материальная точка движется от начального до конечного положения. На рисунке изображен график ее движения. На оси абсцисс откладывается время в секундах, на оси ординат – расстояние от начального положения точки (в метрах). Найдите среднюю скорость движения точки. Ответ дайте в метрах в секунду.
26. Функция y = f(x) определена на промежутке (-6;4). На рисунке изображен график ее производной. Найдите абсциссу точки, в которой функция y = f(x) принимает наибольшее значение.	27. На рисунке изображен график производной функции y=f(x). При каком значении x эта функция принимает свое наибольшее значение на отрезке [-4;- 2] ?	28. На рисунке изображен график производной функции f(x), определенной на интервале (-8;3). В какой точке отрезка [-3;2] функция f(x) принимает наименьшее значение?
29. На рисунке изображен график функции y=f(x), определенной на интервале (-6;8). Определите количество целых точек, в которых производная функции положительна.	30. На рисунке изображён график y=f'(x) — производной функции f ( x), определённой на интервале (−8; 4) . Найдите точку экстремума функции f(x) на отрезке [−3;1].	31. На рисунке изображен график функции y=f(x), определенной на интервале (−5; 5). Определите количество целых точек, в которых производная функции f(x) отрицательна.

32. На рисунке изображен график производной функции f(x), определенной на интервале (−4; 8). Найдите точку экстремума функции f(x) на отрезке [−2; 6].	33. На рисунке изображен график функции y=f(x), определенной на интервале (−2; 12). Найдите сумму точек экстремума функции f(x).	34. На рисунке изображен график производной функции f(x), определенной на интервале (−2; 12). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.
35. На рисунке изображен график производной функции f(x), определенной на интервале (-8;3). В какой точке отрезка [-3;2] функция f(x) принимает наибольшее значение?	36. На рисунке изображен график производной функции f(x), определенной на интервале (−7; 4). Найдите промежутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.	37. На рисунке изображен график производной функции f(x), определенной на интервале (−5; 7). Найдите промежутки убывания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.

⇐ Предыдущая 123 Следующая ⇒