 |
|
Приклад виконання 0-го варіанта задач з теорії ймовірностей
Задача 2.4.
1. Студент знає 46 з 60 запитань програми. Кожний екзаменаційних білет містить 3 запитання. Знайти ймовірність того, що студент знає:
а) всі три запитання;
б) тільки два запитання;
в) тільки одне запитання екзаменаційного квитка.
2. В кожній з двох урн знаходяться 5 білих та 10 чорних кульок. З першої урни переклали у другу навмання 1 кульку, а потім з другої урни вийняли наугад 1 кульку. Знайти ймовірність того, що вийнята кулька виявиться чорною.
3. Три стрільця в однакових та незалежних умовах зробили по одному пострілу по одній і тій самій цілі. Ймовірність влучення у ціль першим стрільцем дорівнює 0,9, другим – 0,8, третім – 0,7. Знайти ймовірність того, що: 1) в ціль зроблено всі три влучення; 2) в ціль зроблено тільки два влучення; 3) тільки одне влучення.
4. Ймовірність, що подія відбудеться у кожному з однакових та незалежних випробувань, дорівнює 0,8. Знайти ймовірність того, що 1600 випробувань подія відбудеться 1200 разів.
5. Для сигналізації про аварію встановлено 3 незалежно працюючих прилади. Ймовірність того, що при аварії спрацює перший прилад, дорівнює 0,9, другий – 0,95, третій – 0,85. Знайти ймовірність того, що при аварії спрацюють:
а) тільки один прилад;
б) тільки два прилади;
в) усі три прилади.
6. Ймовірність настання події у кожному із однакових та незалежних дослідів дорівнює 0,02. Знайти ймовірність того, що в 150 дослідах подія настане 5 раз.
7. В партії з 1000 виробів є десять дефектних. Знайти ймовірність того, що серед 50 виробів взятих навмання з цієї партії 3 будуть дефектні.
8. Ймовірність настання події у кожному із однакових та незалежних дослідів дорівнює 0,08. Знайти ймовірність того, що в 125 дослідах подія наступит не менш ніж 75 і не більш, ніж 90 разів.
9. На трьох пристроях при однакових і незалежних умовах виготовляються вироби однієї назви. На першому пристроі виготовляють 10%, на другому – 30%, на третьому – 60% усіх виробів. Ймовірність кожного з виробів бути бездефектним дорівнює 0,7 – якщо він виробляється на першому пристрої, 0,8 – якщо на другому пристрої, 0,9 – якщо на третьому пристрої. Знайти ймовірність того, що наугад узятий виріб виявиться бездефектним.
10. Два брати належать до складу двох спортивних команд, в кожну з яких входять по 12 чоловік. У двох урнах знаходиться по 12 квитків з номерами від 1 до 12. Члени кожної команди виймають навмання по одному квитку із визначеної урни. Знайти ймовірність того, що обидва брати візьмуть квиток номер 6.
11. З трьох гармат зробили постріли в ціль. Ймовірність попадання в ціль одним пострілом з першої гармати дорівнює 0,8; для другої та третьої гармат ці ймовірності дорівнюють відповідно 0,7 та 0,8. Знайти ймовірність того, що:
а) тільки один снаряд влучить у ціль;
б) рівно два снаряда влучать у ціль;
в) усі три снаряда влучать у ціль;
г) хоча б один снаряд влучить у ціль.
12. Три стрільця в однакових та незалежних умовах зробили по одному пострілу по одній і тій самій цілі. Ймовірність влучення у ціль першим стрільцем дорівнює 0,6, другим – 0,7, третім – 0,9. Знайти ймовірність того, що:
а) тільки один із стрільців влучив у ціль;
б) тільки два влучили у ціль;
в) всі три стрільці влучили у ціль;
г) хоча б один стрілець влучить у ціль.
13. Студент знає 50 з 60 запитань програми. Знайти ймовірність того, що студент знає 2 запитання свого екзаменаційного билета.
14. Дві команди по 10 спортсменів проводять жеребкування для присвоювання номерів учасникам змагань. Двоє братів належать до складу різних команд. Знайти ймовірність того, що обидва брати будуть брати участь у змаганні під номером 5.
15. Два стрільці зробили по одному пострілу по мішені. Ймовірність влучення у мішень кожним з них дорівнює 0,8. Знайти ймовірність того, що:
а) обидва стрільці влучать у мішень;
б) обидва стрільці не влучать;
в) тільки один стрілець влучить.
16. Ймовірність хоча б одного влучення при двох пострілах дорівнює 0,96. Знайти ймовірність трьох влучень при чотирьох пострілах.
17. Експедиція видавництва відправила газети у два поштових відділення. Ймовірність вчасної доставки газет в кожне відділення пошти дорівнює 0,9. Знайти ймовірність того, що:
а) обидва поштових відділення отримають газети вчасно;
б) обидва поштових відділення отримають газети з запізненням;
в) тільки одне поштове відділення отримає газети вчасно;
г) хоча б одне відділення отримає газети вчасно.
18. В кожній з двох урн знаходяться 8 білих та 2 чорних кульки. З першої урни переклали у другу навмання 1 кульку, а потім з другої урни вийняли навмання 1 кульку. Знайти ймовірність того, що вийнята кулька виявиться білою.
19. Два контролери перевірили по однаковому комплекту виробів. Ймовірність того, що перший контролер помилиться дорівнює 0,05; для другого контролера ця ймовірність дорівнює 0,01. При перевірці виробів було знайдено помилку. Знайти ймовірність того, що помилився перший контролер.
20. Ймовірність появи події в кожному з незалежних випробувань дорівнює 0,8. Знайти ймовірність того, що у 100 випробуваннях подія з’явиться не менш ніж 70 і не більш ніж 80 разів.
21. Ймовірність появи події в кожному з незалежних випробувань дорівнює 0,2. Знайти ймовірність того, що подія наступить 20 разів в 100 випробуваннях.
22. Ймовірність появи події в кожному з незалежних випробувань дорівнює 0,8. Знайти ймовірність того, що подія наступить 120 разів в 144 випробуваннях.
23. В кожній з двох урн знаходяться 6 білих та 4 чорні кульки. З другої урни переклали у першу навмання 1 кульку, а потім з першої урни вийняли навмання 1 кульку. Знайти ймовірність того, що вийнята кулька виявиться білою.
24. Ймовірність появи події в кожному з незалежних випробувань дорівнює 0,8. Скільки потрібно провести випробувань, щоб з ймовірністю 0,95 можливо було очікувати відхилення відносної частоти з’явлення події від її ймовірності не більш ніж на 0,02?
25. Ймовірність появи події в кожному з незалежних випробувань дорівнює 0,2. Проведено 900 випробувань. Знайти ймовірність того, що відносна частота появи події відхилиться від її ймовірності не більш ніж на 0,4.
26. Середня кількість літаків, які прибувають в аеропорт за 1 хвилину дорівнює 2. Знайти ймовірність того, що за 3 хвилини прибудуть:
а) 2 літаки;
б) менш ніж 2 літаки;
в) не менш ніж 2-х літаків. В припущенні що потік літаків найпростіший.
27.Середня кількість заявок, що поступають на підприємство побутового обслуговування за одну годину дорівнює 3. Знайти ймовірність того, що за 2 години поступить:
а) 4 заявки;
б) менш ніж 3 заявки;
в) не менш ніж 3 заявки. В припущенні що потік заявок найпростіший.
28. Середня кількість кораблів, які заходять у порт за 1 годину дорівнює 2. Знайти ймовірність того, що за 4 години в порт зайдуть:
а) 5 кораблів;
б) менш ніж 5 кораблів;
в) не менш 5 кораблів.
29. Середня кількість викликів на АТС за 1 хвилину дорівнює 2. Знайти ймовірність того, що за 3 хвилини поступить:
а) 3 виклики;
б) не менш ніж 3 виклики;
в) менш ніж 3 виклики. В припущенні, що потік викликів найпростіший.
30. Середня кількість викликів на АТС за 1 хвилину дорівнює 2. Знайти ймовірність того, що за 4 хвилини потрапить:
а) 3 виклики;
б) не менш ніж 3 виклики;
в) менш ніж 3 виклики. В припущенні, що потік викликів найпростіший.
Задача 2.5.Пристрій складається із трьохнезалежних елементів, які працюють протягом часу Tбезвідмовно з відповідними ймовірностями 
, 
, 
. Знайти ймовірність того, що за час T вийде з ладу:
а) тільки один елемент;
б) хоч би один елемент.
Значення параметрів обчислити за формулами:
, 
, 
, 
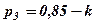, де V –номер варіанта.
Задача 2.6.У першій урні kбілих і lчорних кульок, а у другій урні mбілих і nчорних кульок. Із першої урни навмання виймають r кульок, а із другої – s кульок. Знайти ймовірність того, що серед вийнятих кульок:
а) всі кульки одного кольору;
б) тільки три білих кульки;
в) хоч би одна біла кулька.
Значення k, l, m, n, r, sза варіантами подані у таблиці.
| Варіант | |||||||||||
| K | |||||||||||
| L | |||||||||||
| M | |||||||||||
| N | |||||||||||
| r | |||||||||||
| s |
| Варіант | ||||||||||
| k | ||||||||||
| l | ||||||||||
| m | ||||||||||
| n | ||||||||||
| r | ||||||||||
| s |
| Варіант | ||||||||||
| k | ||||||||||
| l | ||||||||||
| m | ||||||||||
| n | ||||||||||
| r | ||||||||||
| s |
Задача 2.7.У ящику rдеталей, кожна з яких виготовлена за одним із двох видів технологій, причому lіз них – за І-м видом, решта за II-м видом технологій. Ймовірність витримати стендові випробування для деталей кожного з видів технологій відповідно дорівнюють і. Знайти ймовірність того, що випадково взята із ящика деталь витримає стендові випробування. Значення параметрів знайти за формулами:
Задача 2.8.У монтажному цеху до пристрою приєднується електродвигун. Електродвигуни постачаються трьома заводами – виробниками. На складі є електродвигуни з цих заводів відповідно у кількостях М1, М2,і М3штук, які можуть безвідмовно працювати до кінця гарантійного терміну з ймовірностями відповідно 
і .Робітник бере випадково один електродвигун і монтує його до пристрою. Знайти ймовірність того, що змонтований і працюючий безвідмовно до кінця гарантійного терміну електродвигун поставлений відповідно першим, другим або третім заводом – виробником. Значення параметрів обчислюються за такими формулами:
Задача 2.9.Ймовірність виходу зі строю екскаватора у продовж зміни 
. На добувній дільниці кар’єру працює N екскаваторів. Яка ймовірність того, що К з них пропрацює зміну без аварії.
Значення p, N, К наведені нижче у таблиці:
| № вар. | p | N | К | № вар. | p | N | К |
| 0,1 | 0,19 | ||||||
| 0,1 | 0,26 | ||||||
| 0,15 | 0,3 | ||||||
| 0,2 | 0,33 | ||||||
| 0,25 | 0,25 | ||||||
| 0,3 | 0,4 | ||||||
| 0,31 | 0,36 | ||||||
| 0,3 | 0,2 | ||||||
| 0,25 | 0,31 | ||||||
| 0,18 | 0,32 | ||||||
| 0,23 | 0,37 | ||||||
| 0,28 | 0,39 | ||||||
| 0,3 | 0,29 | ||||||
| 0,25 | 0,4 | ||||||
| 0,31 | 0,3 | ||||||
| 0,32 |
Задача 2.10.Змінна продуктивність бурового станка в кар’єрі розподілена за нормальним законом з параметрами а і s. На буровій дільниці працюють n станків. Визначити ймовірність того, що змінна продуктивність бурової дільниці не відрізняється від змінного завдання Пбільше, ніж на 
. Значення а, s, П, n, dподані у таблиці.
| № варіанта | а | s | n | d | П |
Задача 2.11.Серед Nдеталей Мякісних. Вибрали N1деталей. Знайти:
1) Ймовірність того, що серед вибраних деталей М1неякісних;
2) Розподіл випадкової величини Х– числа якісних деталей серед вибраних;
3) Знайти 
і 
-математичне сподівання та дисперсію.
| № варіанта | N | M | N1 | M1 |
Задача 2.12.Знайти ймовірність попадання у заданий інтервал (a, b) нормально розподіленої випадкової величини Х, якщо відоме її математичне сподівання а і середнє квадратичне відхилення s
| № варіанта | a | b | а | s | № варіанта | a | b | а | s |
Задача 2.13.Випадкову величину Хзадано функцією розподілу (інтегральною функцією) F(x). Знайти щільність ймовірності, математичне сподівання, дисперсію. Побудувати графіки інтегральної і диференціальної функції. Знайти 
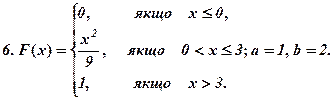
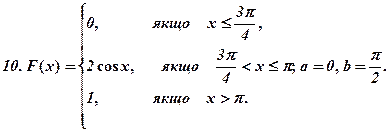
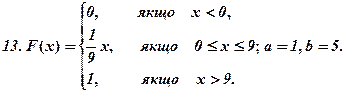
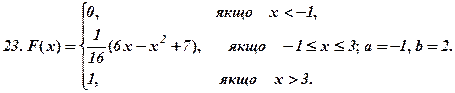
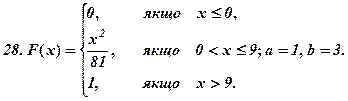
Задача 2.14.Проводиться nнезалежних випробувань. Ймовірність виникнення події 
в кожному випробуванні одна й таж і дорівнює р. Потрібно знайти ймовірність того, що подія з’явиться в цих випробуваннях:
- точно k2 раз;
- не менш k1 і не більшk2раз.
Значення n, p, k1, k2задані за варіантами 1-30.
| №Вар. | n | p | k1 | k2 | №Вар. | n | p | k1 | k2 |
| 0,8 | 0,75 | ||||||||
| 0,2 | 0,8 | ||||||||
| 0,25 | 0,2 | ||||||||
| 0,6 | 0,8 | ||||||||
| 0,5 | 0,009 | ||||||||
| 0,2 | 0,001 | ||||||||
| 0,4 | 0,004 | ||||||||
| 0,25 | 0,006 | ||||||||
| 0,8 | 0,005 | ||||||||
| 0,2 | 0,01 | ||||||||
| 0,75 | 0,005 | ||||||||
| 0,2 | 0,001 | ||||||||
| 0,4 | 0,003 | ||||||||
| 0,8 | 0,5 | ||||||||
| 0,6 | 0,2 |
Задача 2.15.Дискретна випадкова величина Х приймає тільки два значення: х1і х2, причому х1<х2. Відомо: Р(Х=х1)=р1 – ймовірність того, що Х набуде значення, рівне 
; математичне сподівання М(Х)=М и дисперсія D(Х)=D. Потрібно знайти закон розподілу випадкової величини Х. Зробити перевірку розв’язку задачі. З цією метою за знайденим законом розподілу випадкової величини Х підрахувати М(Х) і D(Х).
| № вар. | p1 | М | 
| № вар. | p1 | М |
|
| 0,5 | 1,7 | 0,49 | 0,6 | 1,25 | 0,375 | ||
| 0,25 | 0,7 | 2,2 | 3,36 | ||||
| 0,8 | 2,4 | 0,64 | 0,4 | ||||
| 0,75 | 1,2 | 0,12 | 0,6 | 1,5 | |||
| 0,7 | 2,6 | 0,84 | 0,2 | 1,3 | 0,16 | ||
| 0,6 | 0,7 | 0,06 | 0,4 | ||||
| 0,75 | -2 | 0,7 | 1,9 | 1,89 | |||
| 0,8 | 0,9 | 0,64 | 0,5 | 1,2 | 0,64 | ||
| 0,7 | -0,6 | 0,84 | 0,3 | 0,21 | |||
| 0,4 | 2,5 | 1,5 | 0,6 | ||||
| 0,6 | 1,5 | 1,5 | 0,25 | ||||
| 0,8 | 0,7 | 0,16 | 0,3 | ||||
| 0,4 | 1,3 | 0,06 | 0,8 | ||||
| 0,7 | -0,1 | 1,89 | 0,9 | ||||
| 0,2 | 1,1 | 0,64 | 0,6 | 0,5 | 1/6 |
Задача 2.16.Випадкова величина Хзадана диференціальною функцією розподілу f(x). Знайти інтегральну функцію F(x), математичне сподівання і дисперсію. Побудувати графіки інтегральної і диференціальної функції. Знайти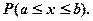
Приклад виконання 0-го варіанта задач з теорії ймовірностей
Задача 2.1.Підкидають три гральні кубики. Знайти ймовірність того, що на верхніх гранях з’явиться число очок, сума яких ділиться на 5.
Розв’язання.Визначимо випробування і його результат, тобто елементарні події. Випробуванням є підкидання трьох гральних кубиків; результат – одна із сполук очок 1, 2, 3, ... ,6 на верхніх гранях трьох кубиків.
Досліджувана подія А – сума очок на трьох кубиках ділиться на 5. Ймовірність події А знайдемо за допомогою формули
Загальну кількість всіх можливих елементарних подій n можна знайти за правилом множення. На кожному гральному кубику 6 граней, кожна з яких може поєднуватись із всіма шістьма гранями на кожному з іншим двох кубиків. Отже, маємо:
Кількість елементарних подій m, що сприяють події А, знайдемо виписавши всі можливі результати випробувань і заливши з них тільки ті, для яких сума очок на всіх трьох гранях ділиться на 5. Можна спростити цю роботу, виписавши всі можливі результати підкидань двох кубиків, сполучаючи з ними відповідні значення кількості очок, що випаде на третьому кубику. Маємо:
113 212 311 366 465 564 663 122 221 316 415 514
613 131 226 325 424 523 622 136 235 334 433 532
631 145 244 343 442 541 636 154 253 352 451 546
645 163 262 361 456 555 654
В результаті отримуємо, що m = 43.
Відповідь: 
Задача 2.2.Слово “математика” складено з карточок,на кожній з яких написано по одній з букв. Після цього карточки перемішуються (всі вони перевернуті тильною стороною до спостерігача) і виймаються без повернення по одній. Знайти ймовірність того, що букви будуть вийматись в порядку заданого слова.
Розв’язання виконаємо двома способами.
І – й спосіб з використанням елементів комбінаторики.
Випробування полягає у випадковому вийманні карточок з буквами без повернення. Елементарними подіями є послідовності букв. Подія А – це отримання слова МАТЕМАТИКА. Кожна з елементарних подій є перестановкою із 10 букв, кількість їх дорівнює 10!
Деякі букви слова МАТЕМАТИКА повторюються (М-2 рази, А-3 рази, Т-2 рази), тому можливі перестановки, при яких слово не змінюється. Їх число дорівнює
m = 2!2!3! = 24.
Отже,
ІІ – й спосібґрунтується на формулі множення залежних подій.
Подія Азалежить від події В, якщо ймовірність появи події А залежить від появи події В. У даному випадку розглядається умовна ймовірність РВ(А)події А за умови, що подія В відбулася. Ймовірність одночасної появи А і В знаходиться за формулою
Р(АВ) = Р(В)РВ(А).
Отже спочатку знаходимо ймовірність першої букви слова
На другому місці повинна бути буква „А” за умови, що буква „М” виставлена, це умовна ймовірність
Тоді
На третьому місці „Т” їх дві у наборі з восьми букв, що залишились, тому умовна ймовірність
Тоді ймовірність частини слова „МАТ” дорівнює
Далі повинна йти буква Е, вона одна серед семи букв, які залишились. Її умовна ймовірність: 
Ймовірність набору чотирьох букв:
Аналогічно для п’ятої букви М
і т.д.
Остаточна ймовірність випадкового набору слова МАТЕМАТИКА дорівнює
Задача 2.3.умова „0” варіанту.
Достатньою умовою складання колоквіуму є відповідь на одне з двох запитань, запропонованих викладачем студентам. Студент не знає відповідей на 8 запитань з 40. Яка ймовірність того, що студент складе колоквіум.
Розв’язання. І – й спосіб.
Знаходимо 
Тоді 
ІІ – й спосіб.Через протилежну подію.
всіх можливих випадків 
.
де 
Задача 2.4.Розв’язування „0” варіанту.
У цеху виготовляють гвинти на 3-х станкахпричому на І -му 25%, на другому – 35%, а ІІІ – 40% усіх виробів. Частка браку серед виробів відносно складає 5, 4, і 2%.
a) Яка ймовірність того, що випадково вибраний гвинт бракований?
б) Випадково вибраний гвинт виявився бракованим. Яка ймовірність того, що його виготовлено на першому, другому, третьому станках?
Розв’язання.а)А – подія, що випадково вибраний гвинт бракований.
Позначимо 
подію – гвинт виготовлений на І –му станку, 
- на І І –му, 
на третьому. Ймовірность цих подій
Р(В1)=0,25; Р(В2)=0,35; Р(В3)=0,4.
Відповідні умовни ймовірності
РВ1(А) = 0,05, РВ2(А) = 0,04, РВ3(А) = 0,02.
Тоді повна ймовірность
б) Випадково вибранний гвинт виявився бракованим (відбулася подія А ). Ймовірність гіпотези, що бракований гвинт виготовлено на І –му станку знаходимо за формулою
Задача 2.5.Пристрій складається із трьох незалежних елементів, які працюють протягом часу Т безвідмовно з відповідними ймовірностями р1, р2і р3. Знайти ймовірність того, що за час t вийде з ладу:
а) тільки один елемент;
б) хоч би один елемент.
Значення параметрів обчислити за формулами:
,
p1 = 1 – k, p2 = 0,9 – k, p3 = 0,85 – k,де V – номер варіанта.
Розв’язання.Оскількі V = 0, то k = 0,149. р1 = 0,851,
р2 = 0,751, р3 = 0,701.
Позначимо через А, В, С – події, що означають безвідмовну роботу відповідно І-го, ІІ-го і ІІІ-го елементів. Згідно умови задачі ймовірності цих подій такі Р(А) = 0,851, Р(В) = 0,751, Р(С) = 0,851.Нехай
відповідні протилежні події, які означають відмову відповідних елементів в роботі, тоді їх ймовірності дорівнюють
1) Розглянемо події, коли виходить з ладу тільки один з елементів (а два інших працюють): 
тобто почергово може відмовити І-й, ІІ-й, або ІІІ-й елементи відповідно. Ці події несумісні, тому якщо позначити через Е – подію „за час Т вийде із ладу тільки один елемент”, то
За теоремою додавання ймовірностей несумісних подій маємо:
Далі до кожного доданка використовуємо теорему множення ймовірностей:
2) Нехай D– подія, яка означає, що „за час Т вийде з ладу хоча б один елемент”, протилежна подія – „не вийде з ладу ні один елемент”, тоді
Відповідь: 1) Р(Е) = 0,418.
2) P(D) = 0.552.
Задача 2.6.У першій урні 6 білих і 4 чорних кульки, а в другій 5 білих і 7 чорних кульок. Із першої урни навмання взяли 3 кульки, а із другої – 2 кульки. Знайти ймовірність того, що серед вийнятих кульок:
а) всі кульки одного кольору;
b) тільки 3 білих кульки;
с) хоча б одна біла кулька.
Розв’язання.Випробуваннями є виймання 3-х кульок із І-ї урни і 2-х кульок із ІІ-ї урни. Елементарними подіями є комбінації по 3 із 10 першої урни і по 2 із 12 кульок другої урни.
а) Знайдемо розв’язок для першої частини. Нехай подія А1 – всі вийняті кульки одного кольору, тобто вони або всі білі, або всі чорні.
Розглянемо всі можливі події:
В1– з першої урни вийняті три білі кульки;
В2 –з першої урни вийняті 2 білі і одна чорна;
В3 – з першої урни вийняті 1 біла і 2 чорних;
В4 – з першої урни вийняті 3 чорних кульки;
F1 –з другої урни вийняті 2 білих кульки;
F2– з другої урни вийняті 1 біла і 1 чорна кульки;
F3 –здругої урни вийняті дві чорних кульки.
Отже, білий колір – це одночасна поява події В1 і F1, тобто В1F1, або В4F3. враховуючи незалежність і несумісність цих подій, отримуємо:
А1 = (В1F1)+( В4F3),
Р(А1)= Р(В1F1)+Р(В4F3).
Знайдемо числа n1 і n2 елементарних подій для І-ї та ІІ-ї урн відповідно. Маємо:
Знайдемо кількість випадків, які сприяють відповідно кожній з елементарних подій
і 
які ми ввели раніше.
Для події В1 кількість сприятливих випадків 
для В2 -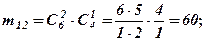 
для В3- 
для В4 -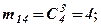 
(для m1i – перший індекс означає номер урни, а другий і – відповідає номеру події Ві ). Далі аналогічно для F1 - 
для F2 - 
для F3 - 
Отже, внаслідок розглянутого маємо
б) Розв’яжемо другу частину задачі. Позначимо через А2 подію „серед взятих 5 кульок із двох урн тільки 3 білих і 2 чорних”. Подія А2 може наступити в результаті появи однієї з подій В1С3, або В2С2, або В3С1, тобто
в) Переходимо до третьої задачі. Нехай подія А3 – „серед вийнятих 5 кульок із двох урн хоча б одна біла”, тоді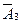 
- протилежна подія: „ні одної білої”, тобто всі кульки чорні. А це суміщення подій В4 і С3, тобто 
Ймовірність 
тоді ймовірність протилежної до 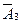події, тобто події А3 дорівнює
Відповідь: 
Задача 2.7.Умова „0” варіанта.
В ящику 19 деталей, кожна з яких виготовлена одним із двох видів технологій, причому 3 із них – за І видом, решта – за ІІ видом. Ймовірність витримати стендові випробування для деталей відповідно 0,81 і 0,46. знайти ймовірність того, що випадково взята із ящика деталь витримає стендові випробування.
Розв’язання.А – подія, що випадково взята деталь витримає стендові випробування. В1 – подія, що взяли деталь з І виду технологій.
В2 – подія, що взяли деталь з ІІ виду технологій.
Використаємо формулу повної ймовірності:
Знайдемо Р(В1),Р(В2). 
Умовні ймовірності дані в задачі: 
Отже:
Відповідь: 0,5153.
Задача 2.8.У монтажному цеху до пристрою приєднуєтьсяелектродвигун. Електродвигуни постачаються трьома заводами – виробниками. На складі містяться електродвигуни цих заводів відповідно в кількості 9, 6 і 11 штук, які можуть безвідмовно працювати до кінця гарантійного строку відповідно з ймовірностями 0,85; 0,76 і 0,71. Робітник бере випадково один двигун і монтує його до пристрою. Знайти ймовірність того, що змонтований і працюючий безвідмовно до кінця гарантійного строку електродвигун виготовлений: першим, другим, третім заводом – виробниками.
Розв’язання.Першим випробуванням є вибір електродвигуна, другим – безвідмовна робота електродвигуна до кінця гарантійного строку.
Розглянемо події:
А –електродвигун працює до кінця гарантійного строку;
В1 – робітник вибирає двигун із продукції І – го заводу;
В2 - робітник вибирає двигун із продукції ІІ – го заводу;
В3 - робітник вибирає двигун із продукції ІІІ – го заводу;
Ймовірності подій 
Ві(І=1,3) знаходяться як відношення числа сприятливих випадків m1=19, m2=6, m3=11 до загального числа всіх можливих випадків (кількість всіх електродвигунів) n=19+6+11=36, тому
Умовні ймовірності події А подані у задачі:
тому
Далі розв’язуємо за формулою Бейєса, тобто обчислюємо ймовірність події (гіпотез) В1, В2, В3, за умови, що подія Авідбулася:
Відповідь: 0,566; 0,160; 0,274.